算法·动态规划

动态规划

  • 状态表示，考虑用几维的状态来表示，背包问题一般为两维f(i,j)，每一个状态的含义

    • 集合（如选法集合）
      • 所有选法
      • 条件
        • 只从前i个物品中选
        • 总体积<=j
    • 属性（如最大值，最小值，数量）

  • 状态计算，如何能把每一个状态算出来

    • 集合划分

      • 如何把该集合划分成更小的子集，使得每一个自己都可以用前面更小的状态表示出来

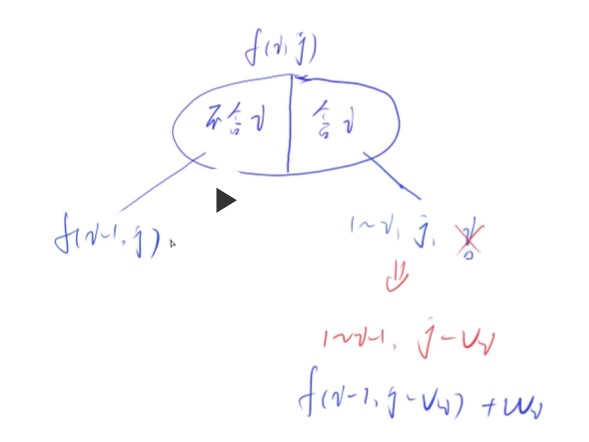
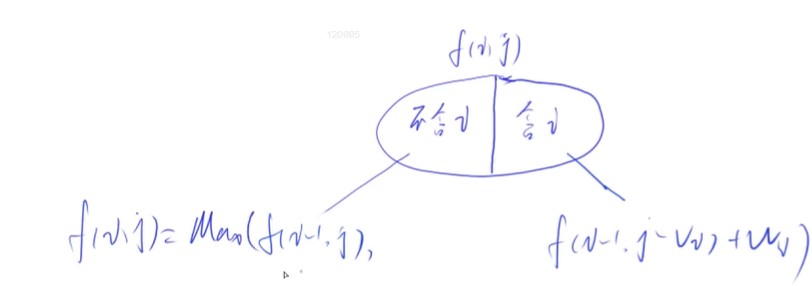
        • 不重复//个数不重复，最大值重复无所谓
        • 不漏

  • DP优化一般是对动态规划的代码或者计算方程进行等价变形

  • DP的集合划分一般考虑最后一步怎么走

  • 动态转移方程涉及到i-1的时候一般下标从1开始比较好

背包问题

总结

  • 01背包
    • N件物品，每件物品只能使用一次
  • 完全背包
    • n种物品，每种物品有无限件可以使用
  • 多重背包
    • n种物品，每种物品最多s件
  • 分组背包
    • n组物品，每组物品最多选一个

01背包

  • N个物品和容量是V的背包，每个物品有体积V和重量W两个属性，每件物品使用1次，要么0次要么1次，求容量内最大价值之和
  • 特点是每件物品最多只用一次
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//二维
#include <iostream>
#include <algorithm>
using namespace std;
const int N =1010;
int n,m;
int v[N],w[N];
int f[N][N];

int main(){
	cin >> n>>m;//读入背包容量和个数 
	for(int i  =1;i<=n;i++)
		cin>>v[i]>>w[i];//读入体积重量 
		
	for(int i = 1;i<=n;i++)
		for(int j = 0;j<=m;j++)
			{
				f[i][j]=f[i-1][j];
				if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
				
			}
			cout<<f[n][m]<<endl;
			return 0;
	
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//一维
#include <iostream>
#include <algorithm>
using namespace std;
const int N =1010;
int n,m;
int v[N],w[N];
int f[N];

int main(){
	cin >> n>>m;//读入背包容量和个数 
	for(int i  =1;i<=n;i++)
		cin>>v[i]>>w[i];//读入体积重量 
		
	for(int i = 1;i<=n;i++)
		for(int j = m;j>=v[i];j--)			
				f[j]=max(f[j],f[j-v[i]]+w[i]);				
			cout<<f[m]<<endl;
			return 0;
	
}

完全背包

  • 每件物品可以用无限次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//朴素版
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int f[N][N];
int main(){
	cin >> n>>m;
	for(int i =1;i<=n;i++) cin >> v[i]>>w[i];
	
	for(int i = 1;i<=n;i++)
		for(int j = 0;j<=m;j++)
			for(int k = 0;k*v[i]<=j;k++)
				f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
	cout<<f[n][m]<<endl;
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//优化版
//朴素版
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int f[N][N];
int main(){
	cin >> n>>m;
	for(int i =1;i<=n;i++) cin >> v[i]>>w[i];
	
	for(int i = 1;i<=n;i++)
		for(int j = 0;j<=n;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
	cout<<f[n][m]<<endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//一维
//优化版
//朴素版
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int f[N];
int main(){
	cin >> n>>m;
	for(int i =1;i<=n;i++) cin >> v[i]>>w[i];
	
	for(int i = 1;i<=n;i++)
		for(int j = v[i];j<=m;j++)//01循环体积从大到小，完全背包问题从小到大
    	    f[j]=max(f[j],f[j-v[i]]+w[i]);
        
	cout<<f[m]<<endl;
	return 0;
}

多重背包问题

  • 每个物品的个数不一样，有个数限制，既不是一件也不是无穷件，而是有一个具体的数值最多有Si个
  • 有朴素版和优化版

朴素版

  • f[i][j]=max(f[i−1][j−v[i]∗k]+w[i]∗k);k=0,1,2,...,s[i]f[i][j]=max(f[i-1][j-v[i]*k]+w[i]*k);k=0,1,2,...,s[i] 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <iostream>
#include <algorithm>
using namespace std;
const int N =110;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main(){
    cin >> n>>m;
    for(int i = 1;i<=n;i++)
        cin >> v[i]>>w[i]>>s[i];
    for(int i =1;i<=n;i++)
        for(int j = 0;j<=m;j++)
            for(int k = 0;k<=s[i] && k*v[i]<=j;k++)
                f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
    cout<<f[n][m]<<endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//优化版，nvlogs
#include <iostream>
#include <algorithm>
using namespace std;
/*二进制优化（下方举例说明）：
①假定物品件数s=200
②二进制形式k[n]={1,2,4,8,16,32,64,73}  其所有值相加是<=200  可以凑出[0~200]的所有数
③除开最后一个数不是二进制形式，73=200-(1+2+4+8+16+31+64)
④其余数，若定64，其中64+[0~63]->[0~127]
⑤最后一个数73，其中73+[0~127]->[0~200] */
const int N =11010,M=2010;
int n,m;
int v[N],w[N];
int f[N];//这里N开的数据范围的依据:多重背包问题中的一个「箱子」相当于01背包问题中的一件「物品」，实际上我们是要将s[i]用几个箱子装进去，因此我们需要估计出多重背包问题中到底有多少个箱子。
                               //这里的箱子也就是二进制优化下的s[i] 由题 s[i]<=2000 则log2000 < 11(log以2为底) 一共最多1000件物品，则我们需要开的范围就是 11*1000+10=11010
int main(){
    cin >> n>>m;//组合方案中的最大价值
    int cnt=0;//重新定义存储物品的编号
    for(int i = 1;i<=n;i++){//循环物品种类
        int a,b,s;
        cin >>a>>b>>s;//输入当前物品的体积，价值，个数
        int k = 1;//定义箱子可以放物品的初始值 第一个箱子可以放一个i号物品
        while(k<=s){//当总数小于最多可选的s件
            cnt++;//编号增加 可以看成是每一个箱子的编号
                v[cnt]=a*k;//这个箱子可以存的i号物品总体积  箱子可以放的物品总数 * 物品体积 = 物品总体积
            	w[cnt]=b*k;
            s-=k;//从总个数s中减去k个
            k*=2;//二进制，乘以二继续循环
        }
        if(s>0){//若总个数s还有剩余，说明此时二进制无法完全覆盖，要找出s即最初s减去二进制综合的个数，即剩余可装多少件
           cnt++;
           v[cnt]=a*s;
           w[cnt]=b*s;
       }
    }
       n=cnt; //关键一步！将物品编号更改为所有物品在箱子里装完后箱子的编号
        //上面结束后 我们将物品全部装进了箱子 我们不管想在背包里装多少个物品i，都可以装箱子的方式实现 
    //例如要装7个物品i 我们就用物品i的1号2号3号箱子(1号能装1个i 2号能装2个i 3号能装4个i) 
    //这就是我们使用二进制优化的意义，能将所有需要的物品数量表示出来
    //由于所有需要的物品数量都能用不同箱子的组合表达 所以现在每个箱子的状态只能是 用或者不用 从而转化为01背包问题

    //对照01背包代码

          for(int i =1;i<=n;i++)//注意n已经被cnt重新赋值了
              for(int j = m;j>=v[i];j--)//01背包逆序存储
                  f[j]=max(f[j],f[j-v[i]]+w[i]);
    cout<<f[m]<<endl;
    return 0;
}

分组背包问题

  • 物品有N组，每一组物品里有若干种，每一组里面最多选一种物品

  • 分组背包是枚举第i组选哪个，多重背包是枚举第i组选几个

  • 转移的时候用的是上一层的状态就从大到小枚举体积，用的是本层就要从小到大枚举体积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
#include <algorithm>
using namespace std;
const in N =110;
int n,mm;
int v[N][N],w[N][N],s[N];
int f[N];
int main(){
    cin >>n>>n;
    for(int i =1;i<=n;i++)
    {
        cin >>s[i];
        for(int j = 0;j<s[i];j++)
            cin>>v[i][j]>>w[i][j];
    }
    for(int i =1;i<=n;i++)
        for(int j = m;j>=0;j++)
            for(int k =0;k<s[i];k++)
                if(v[i][k]<=j)
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
    cout<<f[m]<<endl;
    return 0;
}

线性DP

时间复杂度一般为状态数量*转移计算量

最大最小值可以有重复，数量不可以有重复

数字三角形

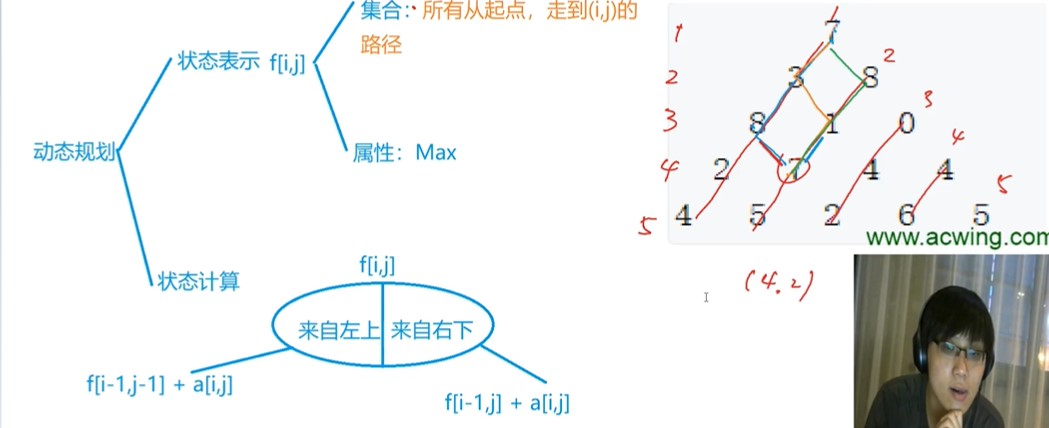
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
#include <algorithm>
using namespace std;
const int N=510,INF=1e9;
int n,m;
int a[N][N];
int f[N][N];
int main(){
  cin >> n;
  for(int i  =1;i<=n;i++)
  	for(int j = 1;j<=i;j++)
  		cin >> a[i][j];
    for(int i=1;i<=n;i++)
        for(int j = 1;j<=i;j++)
            f[i][j]=-INF;
    f[1][1]=a[1][1];
    for(int i =2;i <=n;i++)
        for(int j =1;j<=i;j++)
            f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
    int res=-INF;
    for(int i =1;i<=n;i++)res=max(res,f[n][i]);
    cout<<res;
    return 0;
}

上升子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int n;
int a[N],f[N];
int main(){
    cin >> n;
    for(int i =1;i<=n;i++)
        	cin>>a[i];
    for(int i = 1;i<=n;i++)
    {
        f[i]=1;//只有a[i]一个数
        for(int j =1;j<i;j++)
            if(a[j]<a[i])
                f[i]=max(f[i],f[j]+1);
    }
    int res=0;
    for(int i =1;i<=n;i++)res=max(res,f[i]);
    cout<< res;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//二分优化
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
int a[N];//记录数列
int q[N];//记录单调队列，即q[i]为整个数列的严格单调递增序列，a[i]形状是w，q[i]形状是/

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);//读入数列

    int len = 0;//记录最长子序列长度
    for (int i = 0; i < n; i ++ )//遍历数据
    {
        int l = 0, r = len;//初始化某点最长子序列的长度
        while (l < r)//二分找到小于a[i]的最大值点对应的坐标
        {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) l = mid;
            else r = mid - 1;//l=r返回哪个都一样
        }
        len = max(len, r + 1);//r是小于a[i]的最大值对应的最长子序列的长度，因为a[i]大于q[mid]，所以加上该点长度就是r+1;
        q[r + 1] = a[i];//单调队列记录该值对应的最长子序列的长度
    }

    printf("%d\n", len);

    return 0;
}

最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
#include <algorithm>
using namespace std;
const int N =1010;
int n,m;
int a[N],b[N];
int f[N][N];
int main(){
     cin >> n>>m;
     cin >> a+1>>b+1;
     for(int i =1;i<=n;i++)
     	for(int j =1;j<=m;j++)
     		{
     		f[i][j]=max(f[i-1][j],f[i][j-1]);
     		if(a[i]==b[j])f[i][j]=max(f[i][j],f[i-1][j-1]+1);
     		}
     		cout<<f[n][m];
    return 0;
}

区间DP

石子合并

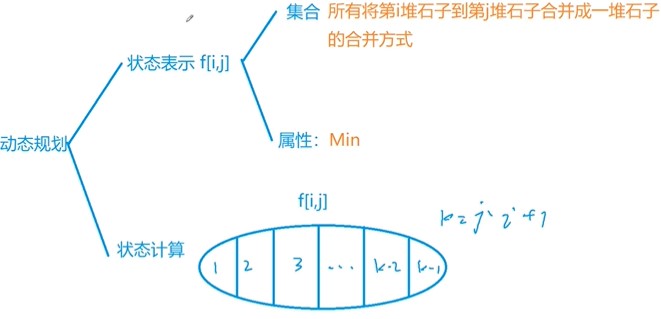
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <algorithm>
using namespace std;
const int N=310;
	int n;
	int s[N];//前缀和
	int f[N][N];//状态数组
	
int main(){
 cin >>n;
 for(int i =1;i<=n;i++)	cin>>s[i];
 	for(int i =1;i<=n;i++) 		s[i]+=s[i-1];
    //状态转移
	for(int len=2;len<=n;len++)//枚举区间长度，一般区间dp问题都是先枚举区间长度，再枚举区间左端点
		for(int i =1;i+len-1<=n;i++){//枚举区间长度下对应的左端点
			int l = i,r=i+len-1;//区间的左右端点
			f[l][r]=1e8;//左右端点对应的最小值初始化
			for(int k = l;k<r;k++)//k在l和r之间
				f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
				
		}
		cout<<f[1][n];
		return 0;
 
}

计数类DP

  • 技巧：当区间不好算的时候就转化为就前缀和

数位统计DP

求出1在每一位上出现的次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 10;

/*
abc x yyy vs abc num[i] efg
001~abc-1, 999

abc
    1. num[i] < x, 0
    2. num[i] == x, 0~efg
    3. num[i] > x, 0~999

*/

int get(vector<int> num, int l, int r)//求出从num中l位到r位的数字
{
    int res = 0;
    for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
    return res;
}

int power10(int x)
{
    int res = 1;
    while (x -- ) res *= 10;
    return res;
}

int count(int n, int x)
{
    if (!n) return 0;

    vector<int> num;
    while (n)
    {
        num.push_back(n % 10);//析出每一位数字
        n /= 10;
    }
    n = num.size();//n为总共的位数

    int res = 0;
    for (int i = n - 1 - !x; i >= 0; i -- )
    {
        if (i < n - 1)
        {
            res += get(num, n - 1, i + 1) * power10(i);
            if (!x) res -= power10(i);
        }

        if (num[i] == x) res += get(num, i - 1, 0) + 1;
        else if (num[i] > x) res += power10(i);
    }

    return res;
}

int main()
{
    int a, b;
    while (cin >> a >> b , a)
    {
        if (a > b) swap(a, b);

        for (int i = 0; i <= 9; i ++ )
            cout << count(b, i) - count(a - 1, i) << ' ';
        cout << endl;
    }

    return 0;
}

状态压缩DP

蒙德里安的梦想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 12, M = 1 << N;//二进制存储，所以要开2^n位

int n, m;
LL f[N][M];// 第一维表示列， 第二维表示所有可能的状态
vector<int> state[M];
bool st[M]; //存储每种状态是否有奇数个连续的0，如果奇数个0是无效状态，如果是偶数个零置为true。

int main()
{
    while (cin >> n >> m, n || m)//读入n,m;
    {//第一部分：预处理1
        //对于每种状态，先预处理每列不能有奇数个连续的0
        for (int i = 0; i < 1 << n; i ++ )//遍历所有方案，即其中一列每一行的01分布状况，i记录的就是一个二进制数，比如i=10010就是记录该列的占领状况
        {
            int cnt = 0;//记录连续的0的个数
            bool is_valid = true;// 某种状态没有奇数个连续的0则标记为true
            for (int j = 0; j < n; j ++ )//遍历这一列，从上到下
                if (i >> j & 1)
                {  //i >> j位运算，表示i（i在此处是一种状态）的二进制数的第j位； 
                     // &1为判断该位是否为1，如果为1进入if
                    if (cnt & 1)
                    { //这一位为1，看前面连续的0的个数，如果是奇数（cnt &1为真）则该状态不合法
                        is_valid = false;//前面是奇数个0，所以该状态不能放入竖放方块
                        break;
                    }
                    cnt = 0;// 既然该位是1，并且前面不是奇数个0（经过上面的if判断），计数器清零。
                    //其实清不清零没有影响
                }
                else cnt ++ ; //否则的话该位还是0，则统计连续0的计数器++。
            if (cnt & 1) is_valid = false; //最下面的那一段判断一下连续的0的个数
            st[i] = is_valid; //状态i是否有奇数个连续的0的情况,输入到数组st中
        }
  //第二部分：预处理2
        // 经过上面每种状态 连续0的判断，已经筛掉一些状态。
        //下面来看进一步的判断：看第i-2列伸出来的和第i-1列伸出去的是否冲突
        for (int i = 0; i < 1 << n; i ++ )//遍历所有方案，即其中一列每一行的01分布状况，i记录的就是一个二进制数，比如i=10010就是记录该列的占领状况
        {
            state[i].clear();//清空上次操作遗留的状态，防止影响本次状态。
            for (int j = 0; j < 1 << n; j ++ )//对于第i列的所有状态
                if ((i & j) == 0 && st[i | j])// 第i-2列伸出来的 和第i-1列伸出来的不冲突(不在同一行) 
                    //解释一下st[j | k] 
                //已经知道st[]数组表示的是这一列没有连续奇数个0的情况，
                //我们要考虑的是第i-1列（第i-1列是这里的主体）中从第i-2列横插过来的，
                //还要考虑自己这一列（i-1列）横插到第i列的
                //比如 第i-2列插过来的是k=10101，第i-1列插出去到第i列的是 j =01000，
                //那么合在第i-1列，到底有多少个1呢？
                //自然想到的就是这两个操作共同的结果：两个状态或。 j | k = 01000 | 10101 = 11101
                //这个 j|k 就是当前 第i-1列的到底有几个1，即哪几行是横着放格子的
                    state[i].push_back(j);
             //二维数组state[i]表示第i行， 
                    //表示 第i列“真正”可行的状态，
                    //如果第i-1列的状态j和i不冲突则压入state数组中的第i行。
                    //“真正”可行是指：既没有前后两列伸进伸出的冲突；又没有连续奇数个0。

        }

        memset(f, 0, sizeof f); //全部初始化为0，因为是连续读入，这里是一个清空操作。
        //类似上面的state[j].clear()

        f[0][0] = 1;// 这里需要回忆状态表示的定义
        //按定义这里是：前第-1列都摆好，且从-1列到第0列伸出来的状态为0的方案数。
        //首先，这里没有-1列，最少也是0列。
        //其次，没有伸出来，即没有横着摆的。即这里第0列只有竖着摆这1种状态。
        for (int i = 1; i <= m; i ++ ) //遍历每一列:第i列合法范围是(0~m-1列)
            for (int j = 0; j < 1 << n; j ++ )//遍历当前列（第i列）所有状态j
                for (auto k : state[j])// 遍历第i-1列的状态k，如果“真正”可行，就转移
                    f[i][j] += f[i - 1][k]; // 当前列的方案数就等于之前的第i-1列所有状态k的累加。

        cout << f[m][0] << endl;//最后答案是什么呢？
        //f[m][0]表示 前m-1列都处理完，并且第m-1列没有伸出来的所有方案数。
        //即整个棋盘处理完的方案数
    }

    return 0;
}

最短hamilton路径

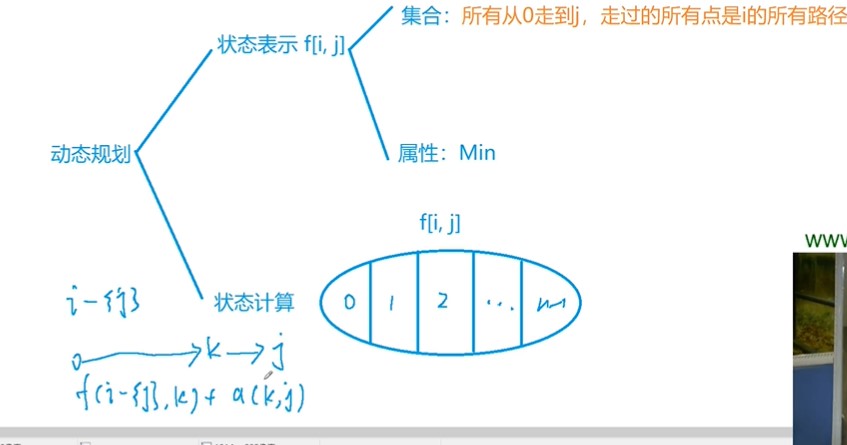
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=20,M=1<<N; //点的选取状态
int n;
int w[N][N];//初始数组
int f[M][N];//dp数组，一维表示路径，二维表示终点。
int main(){
    cin>>n;
    for(int i =0;i<n;i++)
        for(int j=0;j<n;j++)
            cin>>w[i][j];
    memset(f,0x3f,sizeof f);//寻求最小值，初始化大值
        f[1][0]=0;//[1][0]中的0代表终点，1代表路径，自己到自己的路径为0
    for(int i =0;i<1<<n;i++)//i记录路径使用状况，二进制表示
        for(int j=0;j<n;j++)//j表示走到了哪个点
            if(i>>j&1)//路径包含j这个点
                for(int k=0;k<n;k++)//枚举从哪个点转移过来
                    if((i-(1<<j))>>k&1)//路径包含k这个点
                        f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);//终点为k，走过i-1<<j的路径加上k到j的距离
    cout<<f[(1<<n)-1][n-1]<<endl;//(1 << n) - 1 中-1是因为我一开始就为1，要除去 

    return 0;
}

树形DP

没有上司的舞会

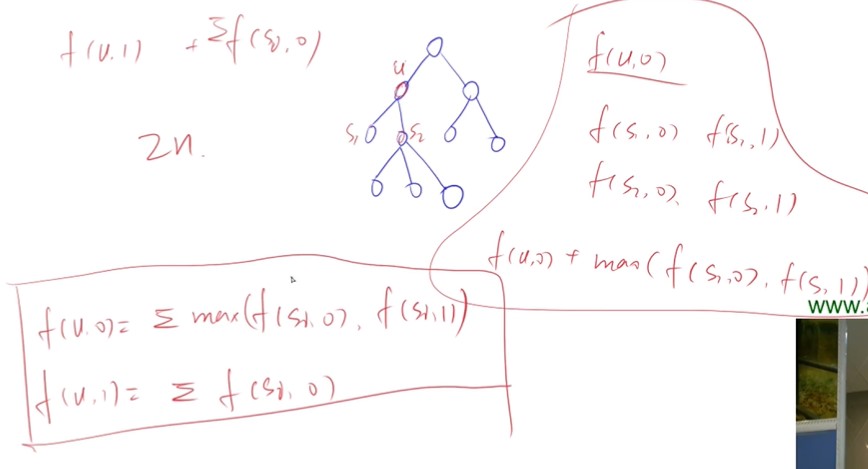
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=6010;
int n;
int happy[N];
int h[N],e[N],ne[N],idx;
int f[N][2];
bool has_father[N];
void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u ){
    f[u][1]=happy[u];
    for(int i =h[u];i!=-1;i=ne[j])
    {
        int j =e[i];
        dfs(j);
        f[u][0]+=max(f[j][0],f[j][1]);
        f[u][1]+=f[j][0];
    }
}
int main(){
    cin >>n;
    for(int i=1;i<=n;i++) cin>>happy[i];
    memset(h,-1,sizeof h);
    for(int i=0;i<n-1;i++)
    {
        int a,b;
        cin>>a>>b;
        has_father[a]=true;
     add(b,a);
    }
    int root =1;
    while(has_father[root])root++;
    dfs(root);
    cout<<max(f[root][0],f[root][1])
        return 0;
}

记忆化搜索

滑雪问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=310;
int n,m;
int h[N][N];
int f[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int dp(int x,int y){
    int &v=f[x][y];
    if(v!=-1)return v;
    v=1;
    for(int i =0;i<4;i++)
    {
        int a=x+dx[i],b=y+dy[i];
        if(a>=1&&a<=n&&b>=1&&b<=m&&h[a][b]<h[x][y]) v=max(v,dp(a,b)+1);
    }
    return v;
    
}
int main(){
cin >>n>>m;
for(int i =1;i<=n;i++)
	for(int j=1;j<=m;j++)
		cin>>h[i][j];
    memset(f,-1,sizeof f);
    int res=0;
    for(int i =1;i<=n;i++)
        	for(int j =1;j<=m;j++)
                res=max(res,dp(i,j));
    cout<<res;
    return 0;
}
算法
#算法
算法·动态规划
http://example.com/2024/03/29/算法·动态规划/
作者
Kugeln
发布于
2024年3月29日
许可协议