算法·搜索与图论

搜索与图论

DFS与BFS

  • DFS用的是stack堆，BFS用的是queue队列，dfs往下搜的时候只需要记录路径上的所有点，因此空间和高度成正比，BFS会把每一层都存下来，所需要的空间是指数级别
  • 当所有边的权重相同的时候BFS第一次搜索到的点一定是最近的一个点，DFS不具有最短路性质
  • 涉及到最小步数，最短距离，最少操作几次基本都是bfs
  • 算法思路奇怪的一般都是dfs，或者对空间要求比较高的

DFS深度优先搜索

  • 最重要的就是顺序，一般是树的形式
  • 回溯一定要注意恢复现场
  • 剪枝：提前判断当前方案是不是合法的，如果不合法可以不用往下走直接回溯
    • 最优解剪枝
    • 可行性剪枝
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//全排列
#include <iostream>
using namespace std;
const int N =10;
int n;
int path[N];//路径数组 
bool st[N];//判断数字有没有被用过 ，初始值为0 
void dfs(int u){

     if(u==n){//当u=n说明已经遍历完毕 ，如果u<n说明还没有填完 
     	for(int i = 0;i<n;i++)
     		cout<<path[i]<<" ";//输出遍历路径 
     		cout<<endl;
     		return ;
	 }
    for(int i = 1;i<=n;i++)//遍历寻找没有被用过的数 
    	if(!st[i]){//!0=1即没有被用过 
    		path[u]=i;//把i填到当前位置
			st[i]=true; 
			dfs(u+1);//继续递归下一个数字 
			st[i]=false;//恢复现场，即将原本填的数字回到没有用过的状态 
		}
} 
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n;
	dfs(0);//u=0的时候位于第一层，即三个位置均为空，u=1位于第二层， 已经填入1or2or3
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//n皇后
#include <iostream>
using namespace std;
const int N =20;
int n;
char g[N][N];
int path[N];
bool col[N],dg[N],udg[N];//col是行，dg是对角线，udg是反对角线 
void dfs(int u){
	if(u==n){
		for(int i = 0;i<n;i++)
			puts(g[i]);
			puts("");
			return ;
	}
	for(int i = 0;i<n;i++)
		if(!col[i]&&!dg[u+i]&&!udg[n-u+i])
		{
			g[u][i]='Q';
			col[i]=dg[u+i]=udg[n-u+i]=true;
			dfs(u+1);
			col[i]=dg[u+i]=udg[n-u+i]=false;
			g[u][i]='.';
		}
}
int main(){
	cin >>n;
	for(int i = 0;i<n;i++)
		for(int j = 0;j<n;j++)
			g[i][j]='.';
	dfs(0);
	return 0;
}

BFS宽度优先搜索

1
2
3
4
bfs最重要的内容：
队列状态表示
队列存入初始状态
定义距离数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bfs常用套路：
int bfs(){
	根据题意定义队列类型（存入数据的类型）
	定义距离数组（新的拓展点到远点的距离）
	上下左右定义
	定义远点距离数组为0
	将原点push进队列
	while(q.size()){
		取出当前的点
		将当前点向周围扩展
		满足条件{
		距离+1；
		将拓展后的点push进入队列
	}
	到达终点，return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
八数码
#include<bits/stdc++.h>

using namespace std;

int bfs(string state)
{
    queue<string> q; //定义队列
    unordered_map<string,int> d; //通过哈希表来让字符串变化时和移动的距离数值关联

    q.push(state); //将字符串入队
    d[state]=0; //将初始状态的字符串的哈希值设定为

    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1}; //定义四个方向向量

    string end="12345678x"; //定义宽度优先搜素的终止状态
    while(q.size()) //循环终止状态
    {
        auto t=q.front(); //将队列中存着的字符串赋值给t
        q.pop(); //队头元素弹出

        if( t==end ) return d[t]; //如果当前字符串等于终止状态搜索结束返回该字符串对应的哈希值
                                  //此处的哈希函数值对应于字符串移动的次数    
        int distance = d[t]; //定义一个临时变量distance存储形成t字符串当前的移动次数
        int k = t.find('x'); //k表示'x'字符在字符串当前的下标
        int x = k/3,y = k%3; //由于字符串当前是一维的将一维下标转化为二维坐标
        for(int i=0;i<4;i++) //分别遍历四个方向
        { 
            int a=x+dx[i],b=y+dy[i]; //将下一个搜索位置的x,y坐标表示
            if(a>=0&&a<3&&b>=0&&b<3) //当二维坐标满足位于3X3矩阵中时
            {
                swap(t[a*3+b],t[k]); //将字符串中的搜索位置与字符'x'交换
                if(!d.count(t)) //如果交换位置后的字符串没有出现过
                {
                    d[t]=distance+1; //将该字符串对应的哈希值在原字符串对应的哈希值基础上加1
                    q.push(t); //将该字符串入队
                }
                swap(t[a*3+b],t[k]); //恢复现场，返回位置判断其他方向
            }
        }
    }

    return -1; //如果无法移动到终止位置返回-1
}

int main()
{
    char s[2];

    string state;
    for(int i=0;i<9;i++)
    {
        cin>>s;
        state+=s; //逐个输入字符串
    }

    cout<<bfs(state)<<endl; //输出宽度优先搜索的数值

    return 0;
}
1
2
3
4
5
queue ←初始化
while queue不空{
t←队头
拓展t
}
1
2
3
4
将一维数组变为二维数组
x=k/n;
y=k%n;
还原 k = x*n+y;

树和图的存储

  • 树是无环连通图

  • 有向图

    • 边有方向

  • 无向图

    • 边没有方向

有向图

邻接矩阵

1
g[a][b] 存储边a->b//如果有权重，g[a][b]就是权重，无权重就是布尔值，不能保存重边，只能保留一条，适合存储稠密图，时间复杂度为O(n)

邻接表

每个节点上开一个表，存一个点可以走到哪个点，插入即找到点对应的单链表然后头插

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[2N], ne[2N], idx;

// 添加一条边a->b
void add(int a, int b)//插入a的邻边
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++ ;//h[a]是头结点，将a节点开头的第一条边变为当前边，idx移动到下一条边
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);
//邻接表的输入
for(int i = 0;i<m;i++)
{
    int a,b;
    cin>> a >>b;
    add(a,b);
}

树与图的遍历

时间复杂度O(n+m)，n表示点数，m表示边数

深度优先遍历

1
2
3
4
5
6
7
8
9
10
11
bool st[N];
int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])//遍历点的边
    {
        int j = e[i];//存储当前链表节点对应的图里面的点的编号
        if (!st[j]) dfs(j);//j没有被搜到，继续搜
    }
}

宽度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
queue<int> q;//初始化
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())//队列不空
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int bfs()
{
	int hh =0,tt=0;//定义队头队尾
    q[0]=1;//q的第一个元素起点
    memset(d,-1,sizeof d);//初始化距离，-1表示没有被遍历过
    d[1]=0;//第一个点遍历
    while(hh<=tt){//队列不空
        int t=q[hh++]//取到队头
            for(int i = h[t];i!=-1;i=e[i])//拓展队头
            {
                int j =e[i];//拓展到队头连接的下一个点
               if(d[j]==-1)//d[j]没有被拓展过
               {
                   d[j]=d[t]+1;
                   q[++tt]=j;
               }
            }
    }
    return 0;
}

树与图的遍历：拓扑排序

时间复杂度O(n+m)，n表示点数，m表示边数

有向图才有拓扑序列，如果有环没有拓扑序，有向无环图一定有拓扑序列，也被称为拓扑图

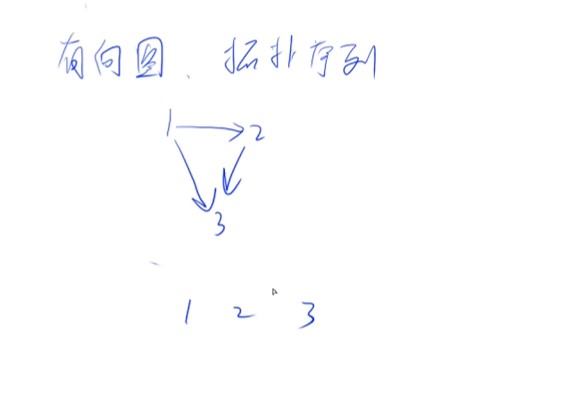
入度是指有多少条边指向自己，因此所有入度为0的点都可以作为起点

出度是指有多少条边出去

  • 把所有入度为0的点入队
    • 一个有向无环图至少存在一个入度为0的点
    • 有向无环图的拓扑序不一定是唯一的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int n,m;
int h[N],e[N],ne[N],idx;
int d[N],q[N];//d[n]表示入度，q[n]是拓扑序列
void add(int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a]=idx++;
    
}
bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;//数组模拟入队

    while (hh <= tt)//队列不空
    {
        int t = q[hh ++ ];//取出来队头

        for (int i = h[t]; i != -1; i = ne[i])//枚举t的所有出边t->j，删掉t->j
        {
            int j = e[i];//找到出边
           d[j]--;
            if ( d[j] == 0)//前面的所有点都已经排好了
                q[ ++ tt] = j;//j入队
         
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}
//出队的顺序就是拓扑序

最短路

  • 源点起点，汇点终点
  • n是点的数量，m是边的数量
  • m和n^n一个级别的叫稠密图
  • m和n一个级别的叫稀疏图
  • 考察的难点在于如何把问题抽象成一个图，如何定义点和边，使得问题能够套入最短路模板
  • 图论侧重于实现

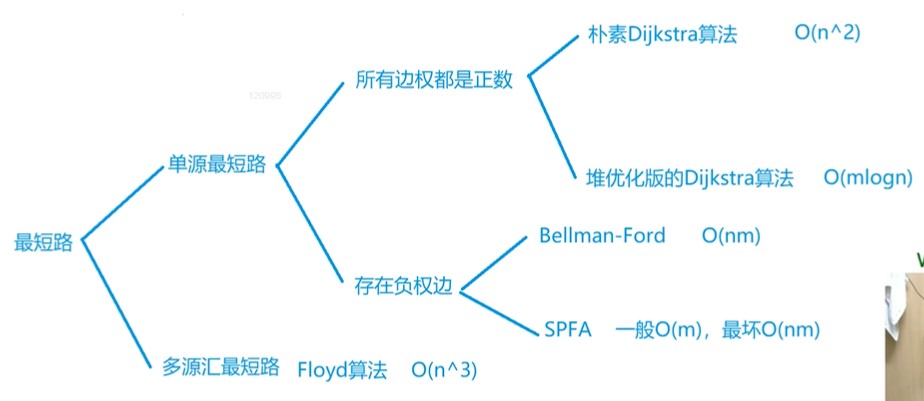
单源最短路

  • 求一个点到其他所有点的最短距离
    • 所有边权都是正数
      • 朴素dijkstra
        • O(n²)，适合稠密图，即边数比较多的时候，如当边数和n²是一个级别的时候
      • 堆优化版dijkstra
        • O(mlogn)，适合稀疏图，如n和m是一个级别的时候
    • 存在负权边
      • bellman-ford O(nm)（存在负环 ）
      • spfa算法 一般：O(m)，最坏O（nm）（不存在负环）
        • 如果限制经过的边数，只能用bellman-ford算法

朴素dijkstra算法

1
2
3
4
5
6
7
思路：
定义距离数组，判断数组，存储结构
初始化距离和存储结构
第一个点的距离定义为0
取出最新点，找出最新点的最短距离
用该最短距离更新
判断长度，得出连不连通
  • 时间复杂度是O(n²+m)，n表示点数，m表示边数
  • 初始化距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int g[N][N];  // 存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//初始化其他距离
    dist[1] = 0;//初始化第一个点的距离

    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;     // 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))//当前点还没有确定最短路；没有赋值或者不是最短的
                t = j;//赋值
  // if(t==n)break;//优化可以加上
        // 用t更新其他点的距离
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);
//判断长度，得出最小距离并更新
        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) //不连通
        return -1;
    return dist[n];
}
//输入输出
cin >> n>>m;
memset(g,0x3f,sizeof g);
while(m--){
    int a,b,c;
    cin>>a>>b>>c;
    g[a][b]=min(g[a][b],c);
}
int t =dijkstra()l
    cout<<t;
return 0;

堆优化版的dijkstra算法

  • 手写堆
  • 优先队列（不支持修改任意一个元素，里面的元素可能是m个，时间复杂度变为mlogm，但由于是稀疏图，所以和mlogn差不多
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
typedef pair<int, int> PII;

int n;      // 点的数量
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N];        // 存储所有点到1号点的距离
bool st[N];     // 存储每个点的最短距离是否已确定

void add(int a,int b,int c){
    e[idx]=b,w[idx]= c,ne[idx]=h[a],h[a]=idx++;
}
// 求1号点到n号点的最短距离，如果不存在，则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//定义小根堆
    heap.push({0, 1});      // first存储距离，second存储节点编号

    while (heap.size())//堆里面非空
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;//编号；距离

        if (st[ver]) continue;//冗余备份
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > distance + w[i])
            {
                dist[j] = distance + w[i];//更新距离
                heap.push({dist[j], j});//放入堆
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
int main(){
    cin >> n>>m;
    memset(h,-1,sizeof h);
    while(m--){
        int a,b,c;
        cin >> a >> b>>c;
        add(a,b,c);
    }
    int t = dijkstra();
    cout<<t;
    return 0;
}

bellman-ford算法

时间复杂度O(mn)，n表示点数，m表示边数

dist[b]<=dist[a]+w 三角不等式

有边数限制的最短路只能用bellman-ford算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int n, m;       // n表示点数，m表示边数
int dist[N];        // dist[x]存储1到x的最短路距离
int bakcup[N];
struct Edge     // 边，a表示出点，b表示入点，w表示边的权重
{
    int a, b, w;
}edges[M];

// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。如果有负权回路，最短路不一定存在。
    for (int i = 0; i < n; i ++ )
    {	
        memcpy(backup,dist,sizeof dist)
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b]=min(dist[b],backup[a]+w)//更新路径，更新的过程叫做松弛操作
        }
    }

    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    return dist[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=510,M=10010;
int n ,m,k;
int dist[N],backup[N];
struct Edge{
	int a,b,w;
	
}edges[M];
int bellman_ford(){
	memset(dist,0x3f,sizeof dist);
	dist[1]=0;
	for(int i = 0;i<k;i++){
		memcpy(backup,dist,sizeof dist);
		for(int j = 0;j<m;j++){
			int a = edges[j].a,b=edges[j].b,w=edges[j].w;
			dist[b]=min(dist[a]),backup[a]+w);
		}
	}
	if(dist[n]>0x3f3f3f3f/2)return -1;
	return dist[n];
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n>>m>>k;
	 for(int i = 0;i<m;i++)
	 	{
	 		int a,b,w;
	 		cin>>a>>b>>w;
			 edges[i] ={a,b,w};
		 }
		 int t =bellman_ford();
		 if(t==-1) puts("impossible");
		 else cout<<t;
		 return 0;
}

spfa算法

图中一定不能有负环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
int n;      // 总点数
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N];        // 存储每个点到1号点的最短距离
bool st[N];     // 存储每个点是否在队列中

// 求1号点到n号点的最短路距离，如果从1号点无法走到n号点则返回-1
void add(int a,int b,int c){
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;//初始化

    queue<int> q;
    q.push(1);
    st[1] = true;//把第一个数放入队列中

    while (q.size())//队列不空
    {
        auto t = q.front();//取出队头
        q.pop();//弹出队头

        st[t] = false;//队头已经弹出

        for (int i = h[t]; i != -1; i = ne[i])//更新t的所有邻边
        {
            int j = e[i];//取出邻边
            if (dist[j] > dist[t] + w[i])//判断能否更新
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])     // 如果队列中已存在j，则不需要将j重复插入
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
spfa判断途中是否存在负环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
int n;      // 总点数
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N], cnt[N];        // dist[x]存储1号点到x的最短距离，cnt[x]存储1到x的最短路中经过的点数
bool st[N];     // 存储每个点是否在队列中

// 如果存在负环，则返回true，否则返回false。
bool spfa()
{
    // 不需要初始化dist数组
    // 原理：如果某条最短路径上有n个点（除了自己），那么加上自己之后一共有n+1个点，由抽屉原理一定有两个点相同，所以存在环。

    queue<int> q;
    for (int i = 1; i <= n; i ++ )
    {
        q.push(i);
        st[i] = true;
    }

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;       // 如果从1号点到x的最短路中包含至少n个点（不包括自己），则说明存在环
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

多源汇最短路

  • 很多不同起点到其他点的最短路

  • Floyd算法O(n^3)

Floyd算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
cosnt int INF=1e9;
初始化：
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;

// 算法结束后，d[a][b]表示a到b的最短距离
void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

最小生成树

最小生成树没有环，正边和负边都没有问题

普利姆算法Prim

朴素版prim

时间复杂度O(n²),n表示点数，m表示边数，稠密图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int n;      // n表示点数
int g[N][N];        // 邻接矩阵，存储所有边
int dist[N];        // 存储其他点到当前最小生成树的距离
bool st[N];     // 存储每个点是否已经在生成树中

//到集合的距离就是一个点连接集合的所有边中最短的那一条
// 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
    memset(dist, 0x3f, sizeof dist);//初始化最短距离

    int res = 0;
    for (int i = 0; i < n; i ++ )//n次迭代
    {
        int t = -1;//不在集合当中的距离最小点的编号
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        if (i && dist[t] == INF) return INF;

        if (i) res += dist[t];//只要不是第一个点
        st[t] = true;

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
    }

    return res;
}

堆优化版

时间复杂度O(mlogn)，稀疏图

克鲁斯卡尔算法Kruskal

时间复杂度O(mlogn),n表示点数，m表示边数

  • 将所有边按照权重从小到大排序
  • 枚举每条边a,b，权重c
    • 如果a，b不连通，将这条边加入集合中来。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int n, m;       // n是点数，m是边数
int p[N];       // 并查集的父节点数组

struct Edge     // 存储边
{
    int a, b, w;

    bool operator< (const Edge &W)const//重载小于号
    {
        return w < W.w;
    }
}edges[M];

int find(int x)     // 并查集核心操作
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);//把所有边排序

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )//从小到大枚举所有边
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);//让a，b分别等于祖宗节点
        if (a != b)     // 如果两个连通块不连通，则将这两个连通块合并
        {
            p[a] = b;//合并两个连通块
            res += w;//存的是最小生成树中所有树边的权重之和
            cnt ++ ;//存的是当前加入了多时少条边
        }
    }

    if (cnt < n - 1) return INF;//图不是联通的
    return res;//输出所有树边的权重之和
}

二分图：染色法、匈牙利算法

染色法

判断一个图是不是二分图

  • 当且仅当图中不含奇数环，奇数环是指边的数量是奇数，二分图是指可以把所有点划分到两边去，使得所有的边都是在集合之间的，集合内部没有边
  • 一条边的旁边两个点颜色一定不同

O(n+m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
int n;      // n表示点数
int h[N], e[M], ne[M], idx;     // 邻接表存储图
int color[N];       // 表示每个点的颜色，-1表示未染色，0表示白色，1表示黑色
void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
// 参数：u表示当前节点，c表示当前点的颜色
bool dfs(int u, int c)//染色邻点过程
{
    color[u] = c;//记录当前节点的颜色
    for (int i = h[u]; i != -1; i = ne[i])//遍历当前点的所有邻点
    {
        int j = e[i];//取出邻点编号
        if (color[j] == -1)//当前点没有染色
        {
            if (!dfs(j, !c)) return false;//dfs(j,!c)染成另外一种颜色，没成功返回false
        }
        else if (color[j] == c) return false;//如果已经染过颜色，判断是不是矛盾，矛盾返回false
    }

    return true;
}

bool check()
{
    memset(color, -1, sizeof color);
    bool flag = true;
    for (int i = 1; i <= n; i ++ )
        if (color[i] == -1)//如果i没有被染色
            if (!dfs(i, 0))//从i开始深度优先遍历图，逐个染色，如果return false，！false=true，说明出现矛盾
            {
                flag = false;//出现矛盾，染色失败
                break;
            }
    return flag;//顺利走到，没有染色失败
}
int main(){
    cin>> n >> m;
    memset(h,-1,sizeof h);
    while(m--){
        int a,b;
        cin >> a >>b;
        add(a,b),add(b,a);
    }
}

匈牙利算法

O(mn)，实际运行时间一般远小于O（mn）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int n1, n2;     // n1表示第一个集合中的点数，n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx;     // 邻接表存储所有边，匈牙利算法中只会用到从第一个集合指向第二个集合的边，所以这里只用存一个方向的边
int match[N];       // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N];     // 表示第二个集合中的每个点是否已经被遍历过

bool find(int x)//能否在另一个集合中找到匹配的
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {//没有匹配或者匹配了但是能够找到另一个匹配的
                match[j] = x;//j是x匹配的点
                return true;//匹配成功
            }
        }
    }

    return false;//匹配失败
}

// 求最大匹配数，依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
    memset(st, false, sizeof st);//清空，使得右边集合中点处于未匹配状态
    if (find(i)) res ++ ;
}

树上启发式合并(DSU on tree)

时间复杂度O（nlogn）

思路：树上启发式合并(DSU on tree)

  • 1.先处理子树大小，类似树链剖分分一下重儿子和轻儿子，为了后续操作降低复杂度
    2.遍历树，对于任何一棵树，先遍历轻儿子，如果有重儿子最后遍历，数据返回的时候只保留重儿子信息，更新颜色出现次数
    3.如果子树颜色出现的最大数 * 最大数次数 = 子树的大小，那么这颗子树就是颜色平衡树，ans ++即可

概念：

  • 重儿子：子树的节点最多的儿子，其中如果两个儿子的子树都相同，那么其中任意个。
    轻儿子：其余的儿子。
    重边：父亲到重儿子的边。
    轻边：其余的边。
    重链：节点到重儿子的路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <iostream>
#include <cstring>

using namespace std;

const int N = 200010 , M = N * 2;

int n;
int h[N], e[M], ne[M], idx;
int color[N], sz[N], son[N], cnt[N];
int res, sum;
int mx;

void add(int a, int b) {//加入点
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

int dfs_son(int u , int father) {
    sz[u] = 1;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if(j == father) continue;
        sz[u] += dfs_son(j , u);
        if (sz[j] > sz[son[u]]) son[u] = j;
    }
    return sz[u];
}

void update(int u, int father , int val, int pson) {//更新
    int c = color[u];
    cnt[c] += val;
    if (cnt[c] > mx) mx = cnt[c], sum = 1;
    else if (cnt[c] == mx) sum ++ ;

    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == pson || j == father) continue;
        update(j, u , val, pson);
    }
}

void dfs(int u, int father , int op) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == son[u] || j == father) continue;
        dfs(j, u , 0);
    }

    if (son[u]) dfs(son[u], u , 1);
    update(u, father , 1, son[u]);

    if (sum * mx == sz[u]) res ++ ;

    if (!op) update(u, father , -1, 0), mx = 0;
}

int main() {
    cin >> n;

    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i ++ ) {
        int p;
        cin >> color[i] >> p;
        if(i != 1)add(p, i) , add(i , p);
    }

    dfs_son(1 , -1);
    dfs(1, -1 , 1);

    cout << res << endl;

    return 0;
}
算法
#算法
算法·搜索与图论
http://example.com/2024/03/26/算法·搜索与图论/
作者
Kugeln
发布于
2024年3月26日
许可协议