算法·基础算法与数据结构

1
2
3
4
ios::sync_with_stdio(0);
cin.tie(0);
//加速cin,cout;
//副作用不能使用scanf,printf

时间复杂度

基础算法

排序

快速排序——分治 O(nlogn)-O(n²)

  • 确定分界点：q[l],q[(l+r)/2],q[r];随机
  • 调整区间：第一个区间所有的数都小于等于x，第二个区间所有的数都大于等于x
  • 递归处理左右两端

快排非稳定，归并稳定（位置不发生变化）

暴力做法

  • a[],b[]

  • q[l-r] q[i]<=x x->a[]

    ​ q[i]>=x x->b[]

  • a[]->q[] b[]->q[]

1
2
3
4
5
6
7
8
9
10
11
12
13
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
 while (i < j)
   {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
   }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

归并排序——分治 O(nlogn)

  • 确定分界点：mid=(l+r)/2
  • 递归排序left,right
  • 归并——合二为一O（n）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];

}

二分

二分不用考虑有没有解

整数二分

  • 有单调性的题目可以二分，但可以二分不一定有单调性，二分的本质不是单调性
  • 二分的本质是性质，使得一部分满足红色性质，一部分满足绿色性质，整个区间可以一分为二，二分可以寻找性质的边界

①红点

  • mid=l+r+1>>1;

    if(check(mid)) true ->[mid,r] l = mid;//mid满足红色性质

    ​ false->[l,mid-1] r = mid-1;//mid不满足红色性质，在绿色性质区域

②绿点

  • mid = l+r>>1;

    if(check(mid)) true->[l,mid] r = mid;//mid满足绿色性质

    ​ false->[mid+1,r] l = mid+1;//mid满足红色性质，不满足绿色性质

1
2
3
4
5
6
7
8
9
10
11
12
13
//mid属于绿色区域
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用，即如果更新方式是r=mid,l=mid+1;
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足绿色性质
        else l = mid + 1;
    }
    return l;
}
1
2
3
4
5
6
7
8
9
10
11
12
//mid属于红色区域
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用,即如果更新方式是l=mid,r=mid-1;
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;//判断mid是否满足红色性质
        else r = mid - 1;
    }
    return l;
}

浮点数二分

注：判断是否满足绿色性质

1
2
3
4
5
6
7
8
9
10
11
12
13
bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求，比要求的位数多2
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

高精度

大整数存法

一般从个位开始存，即a[0]为个位数字，最高位在最后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <iostream>
#include <vector>
using namespace std;
int main(){
    string a,b;
    vector<int> A,B;
    cin >> a >> b;//a="123456"
    for(int i = a.size()-1;i>=0;i--)
        A.push_back(a[i]-'0');//由于字符串里面是字符，需要转化为数字，将a从后往前存入A,A={6,5,4,3,2,1}
    for(int i  =b.size()-1;i>=0;i--)
        B.push_back(b[i]-'0');//由于字符串里面是字符，需要转化为数字，将b从后往前存入B
    for(int i = A.size()-1;i>=0;i--)
        printf("%d",A[i]);
    //输出
}

取位运算

1
2
3
4
5
6
int n;
while(n){
	 cout<<n%10;
	 n/=10;

}//注意，这里先输出高位

字符串转化为数字

1

高精度加法

A、B位数都是10^6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

高精度减法

A、B位数都是10^6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// C = A - B, 满足A >= B, A >= 0, B >= 0
//如果B>A输出-（B-A)
bool cmp(vector<int> &A,vector<int> &B)
{
    if(A.size()!=B.size()) return A.size()>B.size();
    for(int i = A.size()-1;i>=0;i--)
        	if(A[i]!=B[i])
                	return A[i]>B[i];
    return true;
}//判断A是否>=B

vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

高精度乘法

一般为大整数x小整数，大整数的位数一般是小于10^6，小整数的数值一般小于10^9

1
2
3
4
5
6
7
//读入存储
string a;
int b;
cin >> a >> b;
vector<int> A ;
for(int i = a.size()-1;i>=0;i++)
    A.push_back(a[i]-'0');

高精度*低精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;//进位
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);//当前位
        t /= 10;//进位
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

高精度除法

高精度/低精度

1
2
3
4
5
6
7
8
9
10
//读入存储
string a;
int b;
cin >> a >> b;
vector<int> A ;
for(int i = a.size()-1;i>=0;i++)
    A.push_back(a[i]-'0');
//输出
for(int i = C.size();i>=0;i--)
    printf("%d",C[i]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// A / b = C ... r, A >= 0, b > 0,商是c，余数是r
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;//商
    r = 0;//余数
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());//翻转之前C[0]存的是最高位，C[size()-1]存的是最低位，其他是C[0]存的最低位，C[size()-1]存的是最高位，因此需要翻转
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

前缀和与差分

数组a1,a2,a3,a4…an

前缀和

前缀和数组Si=a1+a2+…+ai 下标一定从1开始

  • Si求法

    • for(i = 1;i<=n;i++) s[i]=s[i-1]+a[i];S0=0

  • 前缀和的作用

    • 能快速求出来原数组里一段数的和

      例如计算[l,r]这段的距离，如果没有前缀和数组，时间复杂度为O(n)，如果有前缀和，时间复杂度为O(1)

      [l,r]=s[r]-s[l-1];

一维前缀和
1
2
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]
二维前缀和

1
2
3
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
const int N= 1010;
int n,m,q;
int a[N][N],s[N][N];
int main(){
  scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i<=n;i++)
        	for(int j = 1;j<=m;j++)
                scanf("%d",&a[i][j]);
    for(itn i  =1;i<=n;i++)
        for(int j = 1;j<=m;j++)
            s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];//求前缀和
    while(q--){
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1&y1&x2&y2);
        printf("%d\b",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1]s[y1-1]);//算以(x1,y1)为左上角,(x2,y2)为右下角的子矩阵的和
    }
}

差分

  • a1,a2,a3…an

  • 构造b1,b2,b3…bn

  • 使得 ai=b1+b2+…bi;

  • 即Sbi=ai；

  • 即b1=a1;

    ​ b2=a2-a1;

    ​ b3=a3-a2;

    …

    ​ bn=an-an-1;

  • a是b的前缀和，b是a的差分

  • 作用：

    • 对b数组求一遍前缀和即可求得原数组，时间复杂度为O(n)
    • 如果想要原数组的每一个数都加上一个值，通过差分和前缀和的时间复杂度为O(1)
      • Bl+c，后面的Al-An全部都会加上C ，如果想要只发生在l-r，则Br+1 - C
一维差分
1
给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c
二维差分

1
2
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
using namespace std;
const int N =1010;
int n,m,q;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}
int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);//读入二维数组
    for(int i = 1;i<=n;i++)
        for(int j = 1; j<=m;j++)
            insert(i,j,i,j,a[i][j]);//插入前缀和，构造差分数组
    while(q--)
    {
        int x1,y1,x2,y2,c;
        cin >> x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);   //插入操作,在差分数组的特定位置进行操作
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
    for(int i = 1;i<=n;i++)
    {
        for(int j = 1;j<=m;j++) printf("%d ",b[i][j]);
        puts("");
    }
    return 0;
    
}

双指针算法

  • 两个序列，一个指针指向第一个序列，另一个指针指向第二个序列
  • 一个序列，一个指针指向开头，一个指针指向结尾
  • 所有的双指针算法时间复杂度都是O(n)
1
2
3
4
5
6
7
8
9
for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 以下是具体问题的逻辑
}
//常见问题分类：
//    (1) 对于一个序列，用两个指针维护一段区间
//    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

  • 核心思想：

    • for(int i = 0;i<n;i++)

      ​ for(int j =0;i<n;j++)

      ​ O(n^2)

    ​ 将上面的朴素算法优化到O(n)

  • 一般先思考暴力做法，然后看i和j之间有没有单调关系，利用单调关系改变时间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//例：把每个单词分别输出出来
#include <iostream>
#include <cstring>
using namespace std;
int main(){
    char str[1000];
    fgets(str);
    int n = strlen(str);
    for(int i = 0;str[i];i++){
        int j = i;
        while(j<n&&str[j]!=' ')j++;
      
        //以下这道题的具体逻辑
        for(int k  = i;k<j;k++)
            cout<<str[k];
        cout<<endl;
        i=j;
    }
}

位运算

  • 求n的二进制表示中第k位数字是几，个位是第0位，从右往左算
    • 先把第k位移到最后一位
      • n>>k;
    • 看一下个位是几
      • x&1;
1
n>>k&1

lowbit(x):返回x的最后一位1

1
2
3
4
5
6
例：
int lowbit(int x){
    return x&-x;
}
x=1010;
lowbit(x)=10;
  • 原码 1010
  • 反码 取反
  • 补码 取反加一（计算机里的负数用补码来表示）

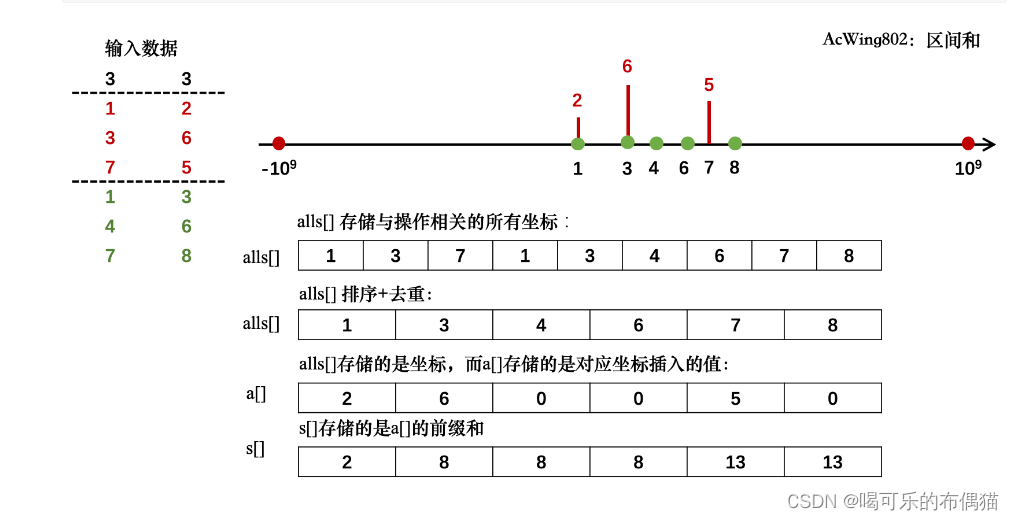
离散化

值域大，个数少

问题：

  • a中可能有重复元素，需要去重
  • 如何算出ai离散化后的值
    • 二分
  • 保序离散化，小的在前面大的在后面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素
//alls存储的是坐标，而a[]存储的是离散化后的坐标插入的值，s[]存储的是a[]的前缀和
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{//因为alls已经去重排序，所以alls里面的数对应的下标，就是离散化以后对应的坐标，找alls里面大于等于x的最大值的坐标，就是找离散化后的坐标
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n  不加1从0开始映射
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
//例题：区间和
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 300010;

int n, m;
int a[N], s[N];

vector<int> alls;
vector<PII> add, query;

int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});

        alls.push_back(x);
    }

    for (int i = 0; i < m; i ++ )
    {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);
    }

    // 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());

    // 处理插入
    for (auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }

    // 预处理前缀和
    for (int i = 1; i <= alls.size(); i ++ ) s[i] = s[i - 1] + a[i];

    // 处理询问
    for (auto item : query)
    {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

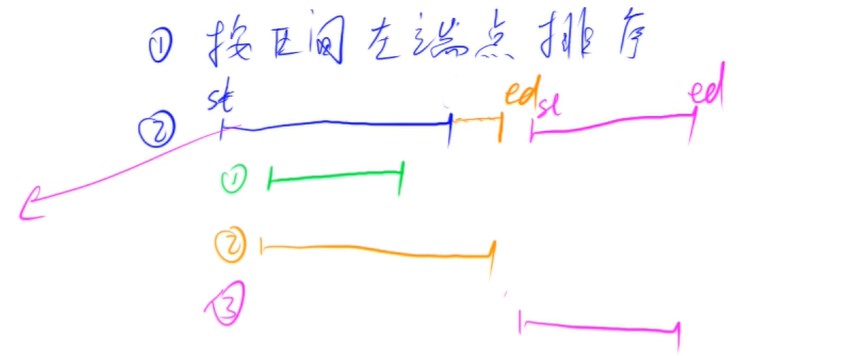
区间合并

  • 按区间左端点排序
  • 扫描整个区间，把所有可能有交集的区间合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
    vector<PII> res;

    sort(segs.begin(), segs.end());

    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        if (ed < seg.first)
        {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);

    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}

数据结构

链表与邻接表：树与图的存储

单链表（数组模拟）(静态链表)

常用邻接表，存储树和图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;//e为节点的值，ne为指向的地址
//因为是从0开始的，所以第k的插入点的下标是k-1
// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 在链表头插入一个数a，即头插法
void insert(int a)
{
    e[idx] = a, ne[idx] = head, head = idx ++ ;//idx即新插入的点的下标
}

//将x插入到下标是k的点的后面
void add(int k ,int x)
{
    e[idx] = x;
    ne[idx]=ne[k];
    ne[k]=idx++;
    
}

//将下标是k的点后面的点删掉
void remove(int k){
    ne[k]=ne[ne[k]];
}


// 将头结点删除，需要保证头结点存在
void remove()
{
    head = ne[head];
}

//遍历单链表
for(int i = head;i!=-1;i=ne[i])
    	cout<<e[i]<<endl;

struct版在408（1），struct创建新链表比较慢

双链表（数组模拟）（静态链表）

常用于优化某些问题

双链表即一个节点指向左右

初始化

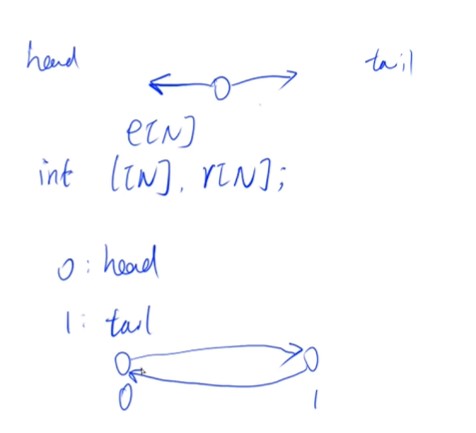
右插

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化
void init()
{
    //0是左端点，1是右端点，即0是头结点，1是尾结点
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

栈与队列：单调队列、单调栈

栈（先进后出）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// tt表示栈顶
int stk[N], tt = 0;//stk表示栈，tt表示栈顶下标

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空，如果 tt > 0，则表示不为空
if (tt > 0) not empty;
else empty;

//栈顶
stk[tt];
中缀表达式
1

单调栈
  • 单调栈和单调队列都是用栈和队列暴力模拟问题，即找出朴素算法，再看一下没用的元素，删掉元素看是否有单调性，有单调性可以用单调队列或者单调栈优化问题，取极值直接找两个端点，找一个点可以用二分
1
2
3
4
5
6
7
//常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;//当栈不为空且当前元素符合某种性质，不会用到当前元素
    stk[ ++ tt] = i;
}//时间复杂度为O(n)

队列（先进先出）

普通队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

//取出队尾
q[tt];

// 判断队列是否为空，如果 hh <= tt，则表示不为空
if (hh <= tt) not empty;
    else empty;

循环队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;

// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;

// 队头的值
q[hh];

// 判断队列是否为空，如果hh != tt，则表示不为空
if (hh != tt)
{

}

单调队列
  • 队列里面存的是下标
1
2
3
4
5
6
7
8
//常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;//插入值
}

kmp

思路：

  • 暴力算法怎么做

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    s[N],p[M];//s是主串，p是模板串

    for(int i = 1;i<=n;i++){
    //
    bool flag = true;

    for(int j = 1;j<=m;j++)

    if(s[i+j-1]!=p[j]){//因为匹配的时候指向s的也要往后挪动，所以这里的[]内是指s的本轮循环的位置还要往后挪多少位置，最开始的时候是初始位置对比字串，所以挪动的位置为0，此后要-1来保持对准

    flag = false;

    break;
    	}

    }

  • 如何去优化

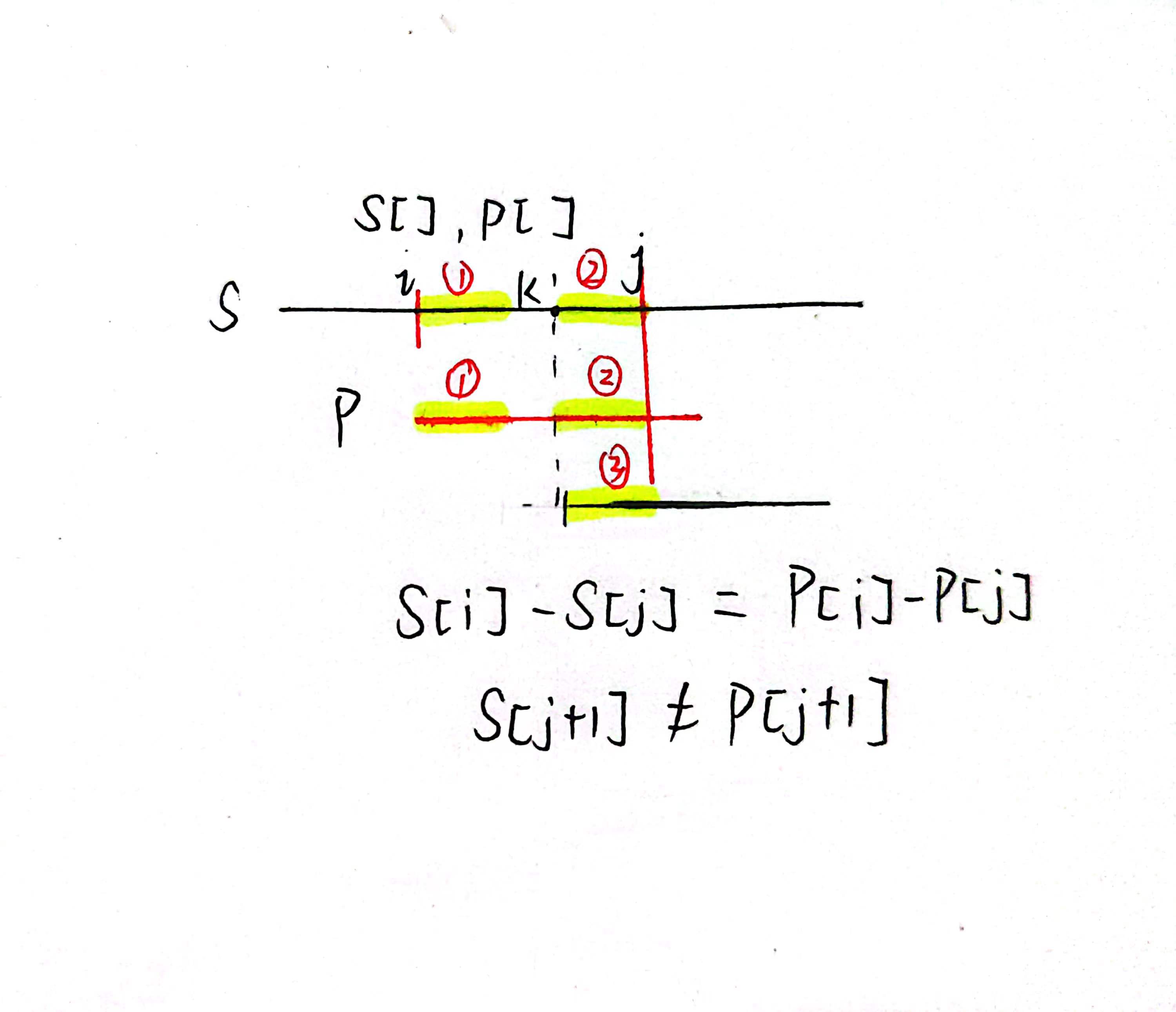
存在五个相等的轴，其中：

  • 由于第一段第二段在i-j都相等，所以P①=S①，P②=S②
  • 由于J+1匹配失败，P字串向后移动直到再次匹配，此时P③=S②，由于S②=P②，所以P②=P③
  • 由于P实际上为字串位移，所以P③=P①
  • 综上，存在五段相等的轴
  • 因此，只需要求子串P中，P①=P②的最大区域，当该区域越大， P再次匹配往后移动的距离越短

因此，对于字串P：

  • 需要预处理出以某个点为终点的后缀与前缀相等，相等的长度最大为多少

    1
    Next[i]=j//即从i开始的后缀与从1开始的前缀相等，而且后缀的长度最长
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// s[]是长文本，p[]是模式串，n是s的长度，m是p的长度 s[]要匹配的长串，p[]比较短的模板串
求模式串的Next数组：
for (int i = 2, j = 0; i <= m; i ++ )//扫描p的长度
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

// 匹配O(n)
for (int i = 1, j = 0; i <= n; i ++ )//扫描s的长度
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        // 匹配成功后的逻辑
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//完整
#include<iostream>
using namespace std;
const int N =10010,M=100010;
int n ,m;
char p[N],s[M];
int ne[N];

int main(){
	
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n>>p+1>>m>>s+1;
	//求next数组的过程
	for(int i = 2,j=0;i<=n;i++){
		while(j&&p[i]!=p[j+1]) j = ne[j];
		if(p[i]==p[j+1])j++;
		ne[i] = j;
	}
	
	
	 
	//kmp匹配过程
	for(int i = 1,j=0;i<=m;i++) //i枚举Si ，j和Si匹配的是P(j+1) ,总往前错一位 
	{
		while(j&&s[i]!=p[j+1])//j没有退回起点，退回起点意味着要重新开始匹配 ;不等意味着那个位置不匹配了 
	    	j = ne[j];//ne[j]是当前j点的最长后缀的长度，j是不匹配后往后移动更新的检验分界点。由于j从0开始，所以当j等于上一个j的ne长度时，相当于j被更新到图示位置 
	    if(s[i]==p[j+1]) j++;//下一个字符终于匹配，继续检验下一个位置的字符是否匹配 
		if(j==n) {
			//匹配成功 
			cout<<i-n<<" ";
			j=ne[j];
		}
	}
	
	
}

kmp匹配过程

求next数组的过程

完整过程

Trie

支持两个操作：

  • 高效地存储和查找字符串集合的数据结构
    • 字符类型和个数不会很多，要么都是大写要么都是小写要么都是数字
  • trie树的存储

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点的坐标
// cnt[]存储以每个节点结尾的单词数量
//idx存储当前用到了哪个下标，下标是0的点，既是根节点又是空节点

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';//a-z映射成0-25
        if (!son[p][u]) son[p][u] = ++ idx;//不存在对应字母就创建出来，u是要存的字母在26个字母中对应的位置
        p = son[p][u];//p的坐标变为当前点的下一个字母对应的坐标，如要插入abcd，之前p在根节点，为son[0][0]，现在son[0][0]已经插入++idx，即son[0][0]=1，所以此时p变为1，转到a开始寻找a的子节点。
    }
    cnt[p] ++ ;//以这个点为结尾的单词数量多了一个
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';//找到当前字母对应的子节点的编号
        if (!son[p][u]) return 0;//查找发现不存在
        p = son[p][u];//继续往下走
    }
    return cnt[p];//返回以p结尾的单词数量
}

并查集

  • 快速处理

    • 将两个集合合并

    • 询问两个元素是否在一个集合当中

    • 近乎O(1)

    • 用树的形式维护所有集合，根节点的编号就是集合的编号，每个节点都存储一个父节点p[x]，当要查找元素属于哪个集合，只要找到根节点的编号即可。

      • 如何判断是否是树根：if(p[x]==x)

      • 如何求x的集合编号:while(p[x]!=x)x=p[x];//只要不是树根就一直往上走，直到走到树根为止

        • 优化：路径压缩

      • 如何合并两个集合

        px是x的集合编号,py是y的集合编号。p[x]=y;

  • 读入操作

    char op[2];

    scanf(“%s”,op) 用字符串不会读入空格和回车

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
(1)朴素并查集：

    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点，即所在集合的编号，顺便加上路径优化
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);//当不是祖宗节点的时候，寻找父节点的父节点，递归之后找到祖宗节点并将路径优化
        return p[x];//返回祖宗节点
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);//让a的祖宗节点的父节点等于b的祖宗节点，即将a插入b中

    //判断a和b是不是在同一个集合中
      if(find(a)==find(b)) puts("yes");
		else puts("no"); 

(2)维护size的并查集：

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量，只保证根节点的size有意义

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
      if(find(a)==find(b))continue;//a和b在一个集合当中
    size[find(b)] += size[find(a)];//把a集合中点的个数加到b集合中
    p[find(a)] = find(b);//将a插入b
    //找到某点所在的集合的点的个数
      cout<<size[find(a)];

(3)维护到祖宗节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

堆

  • 功能

    • 插入一个数
    • 求集合当中的最小值
    • 删除最小值
    • 删除任意一个元素
    • 修改任意一个元素

  • 堆是一颗完全二叉树，除了最后一层节点外，上面的节点都是满的，最后一层从左到右排列

建堆：

1
//小根堆：每一个点小于等于左右子节点，根节点是整个数据结构中的最小值，用一维数组来存，stl里的堆是优先队列

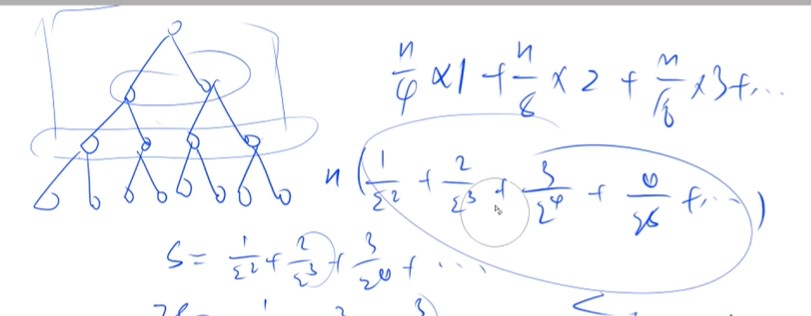
建堆时间复杂度解释

堆的高度最高是logn层

  • heap_swap示意图

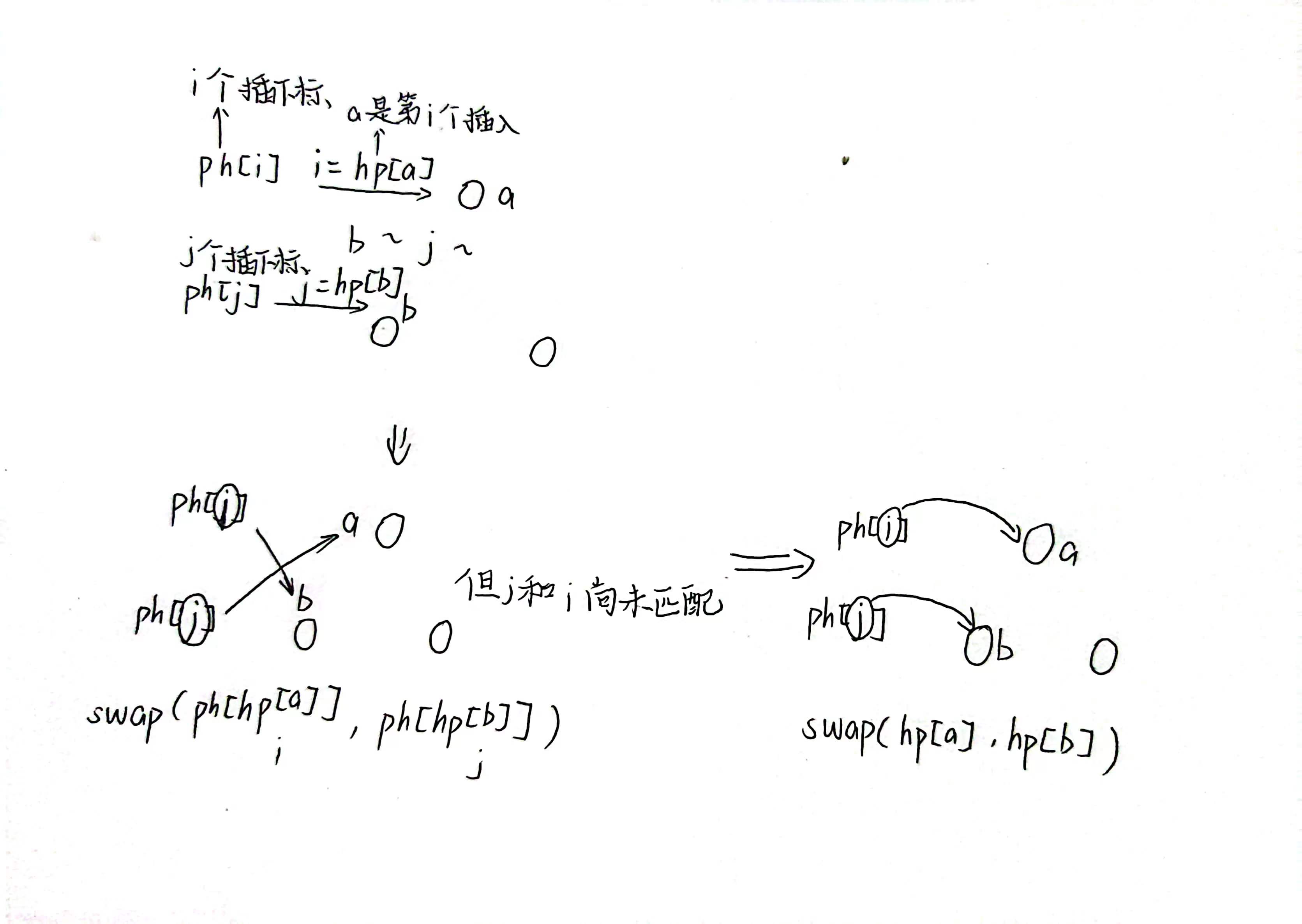
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// h[N]存储堆中的值, h[1]是堆顶，x的左子节点是2x, 右子节点是2x + 1
// ph[k]存储第k个插入的点在堆中的位置，即下标
// hp[k]存储堆中下标是k的点是第几个插入的
//hp[]和ph[]互为反函数
int h[N], ph[N], hp[N], size;

// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);//hp[a]即下标是a的点是第几个插入的，hp[b]即下标是b的点是第几个插入的，即hp[a]和hp[b]都是ph[k]中的k，因此ph[hp[a]]和ph[hp[b]]就是找a和b在堆中的位置，swap即交换他们之间的位置，即交换下标 。
    swap(hp[a], hp[b]);//因为堆中的位置发生变化，即他们在堆中的下标也发生变化，相应的hp[k]，即存储堆中下标是k的点是第几个插入的对应数字也发生变化，需要重新匹配，即交换k对应的插入次序
    swap(h[a], h[b]);//交换值
}

void down(int u)//往下调整，时间复杂度O(logn)
{
    int t = u;//t代表三个数中最小值的点坐标
    if (u * 2 <= size && h[u * 2] < h[t]) //判断是否存在左节点，判断左节点是否小于该节点
        t = u * 2;//当左节点小于该节点，将t变成左节点
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t])//判断右节点是否存在；判断右节点是否小于目前的最小点（如果上面成立，最小点已经更新为左节点） 
        t = u * 2 + 1;
    if (u != t)//说明根节点不是最小值，需要进行交换
    {
        heap_swap(u, t);//将t（保存的最小值的坐标）变成根节点，将t变成原根节点。
        down(t);//将原根节点往下沉进行递归处理直到合适的位置
    }
}

void up(int u)//往上调整，每次往上走只需要跟父节点比较，时间复杂度O(logn)
{
    while (u / 2 && h[u] < h[u / 2])
        //存在父节点；父节点比当前节点大，说明该子节点应该向上
    {
        heap_swap(u, u / 2);//交换父子节点，即原子节点已经变成新的父节点
        u >>= 1;//跳转到新的父节点的坐标，继续进行递归操作
    }
}

// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);//由于从下往上递归，在down的时候可以保证每个根节点的左右节点都是完好无损的

//插入一个数
heap[++size]=x;up(size);

//求当前队列的最小值
heap[1];

//删除一个最小值，即删掉堆顶元素:用整个堆的最后一个元素覆盖掉 ，因为是用数组的形式进行存储，删除数组前面的数比较困难，删除最后一个数比较简单 
heap[1]=heap[size];//用最后一个元素覆盖掉堆顶元素
size--;//删除最后一个元素
down(1);//重新排序堆

//删除任意一个元素
heap[k]=heap[size];//用最后一个元素覆盖掉要删除的元素
size--;//删除最后一个元素
down(k);up(k);//只会执行一个

//修改一个元素
heap[k]=x;
down(k);up(k);

Hash表

  • 存储结构

    • 开放寻址法

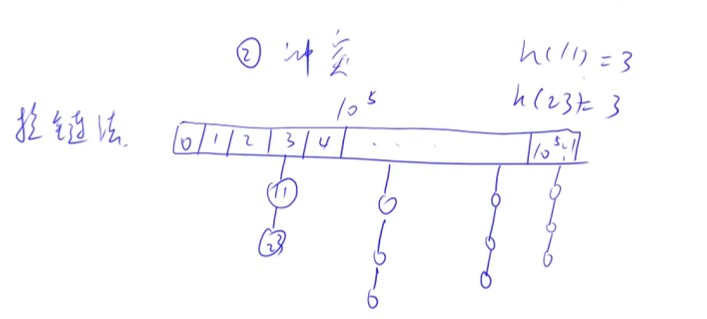
    • 拉链法

  • 字符串哈希

  • 作用：把一个比较庞大的空间（值域）映射到比较小的空间，映射后的函数叫做哈希函数

    • x %10^5 ∈(0,10^5)
      • 模的数一般要取成质数，所以一般要遍历寻找最小的质数
    • 冲突：两个不一样的数映射成了同一个数，处理冲突的方式可以分为开放寻址法和拉链法

拉链法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
(1) 拉链法
    int h[N], e[N], ne[N], idx;//h[N]是槽，e[N]（值）、ne[N]（下一个位置）是链表
//memset(h,-1,sizeof h)把槽先清空
    // 向哈希表中插入一个数
    void insert(int x)
    {
        int k = (x % N + N) % N;//把余数变成正数，k就是x的哈希值，将x插到k槽的单链表中
        e[idx] = x;//存下x的值
        ne[idx] = h[k];
        h[k] = idx ++ ;//链表插入操作
    }

    // 在哈希表中查询某个数是否存在
    bool find(int x)
    {
        int k = (x % N + N) % N;//求出哈希值定位槽位置
        for (int i = h[k]; i != -1; i = ne[i])//遍历单链表
            if (e[i] == x)//判断该槽链表中是否存在x
                return true;

        return false;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//寻找质数
for(int i =  ; ;i++){
bool flag =true;
for(int j = 2;j*j<=i;j++)
	if(i%j==0){
	flag =false ;
	break;
	}
	if(flag)
	{
	cout<<i<<endl
	break;
	}
}

开放寻址法

  • 只开一个数组，但是开的长度一般是输入数据的2-3倍
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(2) 开放寻址法
    int h[N];
//需要定义一个不在数据范围内的null，如0x3f3f3f3f，一般设置最大值,INT_MAX也还是0x3f3f3f3f

memset(h,0x3f,sizeof h);//初始化哈希表
    //由于x是int类型，一个int四个字节，相当于4个3f，即0x3f3f3f3f

// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
    int find(int x)
    {
        int t = (x % N + N) % N;//求哈希值，即映射
        while (h[t] != null && h[t] != x)//t位置上面有人，并且位置上的值不等于x
        {
            t ++ ;//看下一个位置
            if (t == N) t = 0;//看完了最后一个位置，需要循环看第一个位置
        }
        return t;//如果x在哈希表中，返回的就是x的下标，如果x不在哈希表中，返回的就是x应该插入的位置
    }

//插入一个数字
h[find(x)]=x;
//判断数字是否在哈希表中
if(h[find(x)])== null cout<<"No";
else cout<<"Yes";

字符串哈希

字符串前缀哈希法

  • 先预处理出所有前缀的哈希

    把字符串看成是p进制的数字，每一位上的字母就表示p进制上的每一位数字，然后再取模，就可以把字符串映射到从0到Q-1

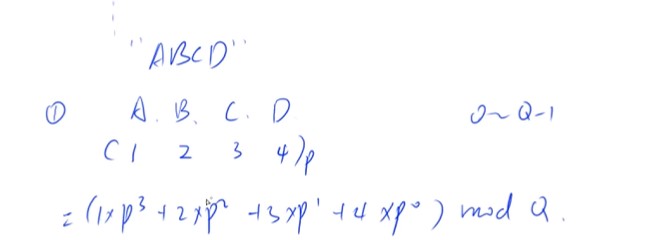
  • A-Z不能映射成0，一般从1开始

  • 字符串哈希假定不存在冲突，因此不考虑冲突

  • 好处是可以利用前缀哈希算出来任意一个子串的哈希值

  • 作用：

    快速判断两个字符串是否相同，哈希值相同，两个字符串相同，如果哈希值不同，则两个字符串不同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
核心思想：将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
小技巧：取模的数用2^64，这样直接用unsigned long long存储，溢出的结果就是取模的结果

typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
const int P=131 or 13331 //P进制
// 初始化
p[0] = 1;//p的零次方等于1
for (int i = 1; i <= n; i ++ )
{
    h[i] = h[i - 1] * P + str[i];
    p[i] = p[i - 1] * P;//位数对应的数字，类似于024816
}

// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

树状数组

  • O（logn)
  • 可以动态地给某个位置上的数加上一个数（单点修改）
  • 求某一个前缀和（区间查询）
  • 奇数位置存的都是原数组（第0层）

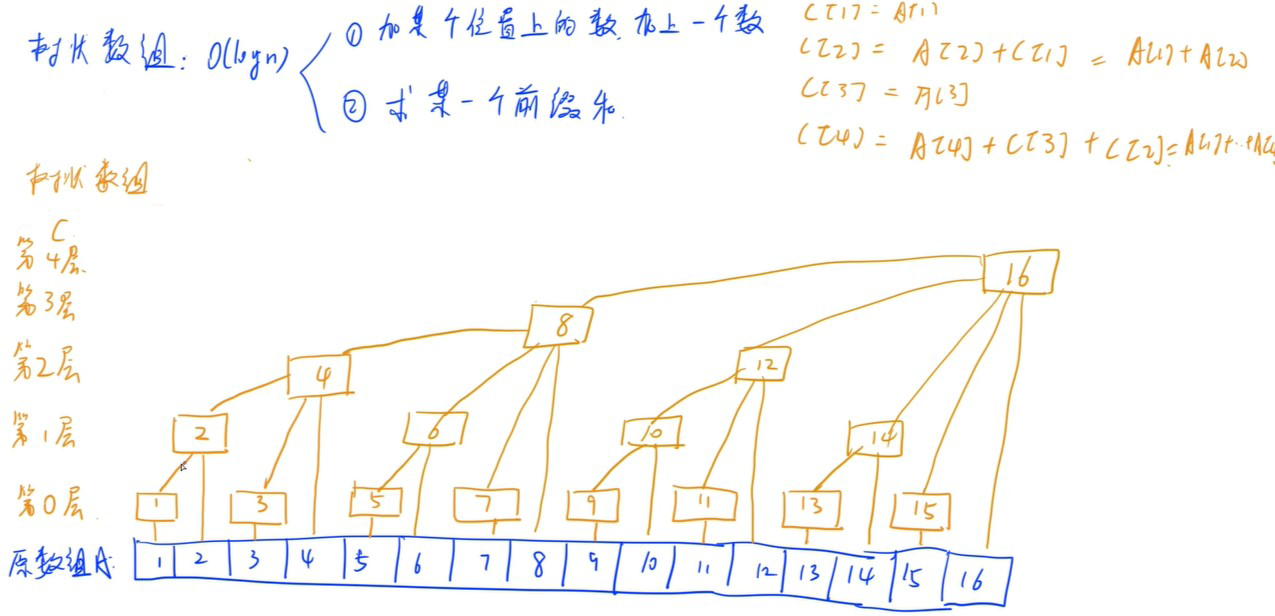
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int a[N], tr[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int v)//a[x]+v，更新前缀和
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

int query(int x)//求到x的前缀和
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) add(i, a[i]);

    while (m -- )
    {
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        if (k == 0) printf("%d\n", query(y) - query(x - 1));
        else add(x, y);
    }

    return 0;
}

线段树

  • 单点修改（Ologn）

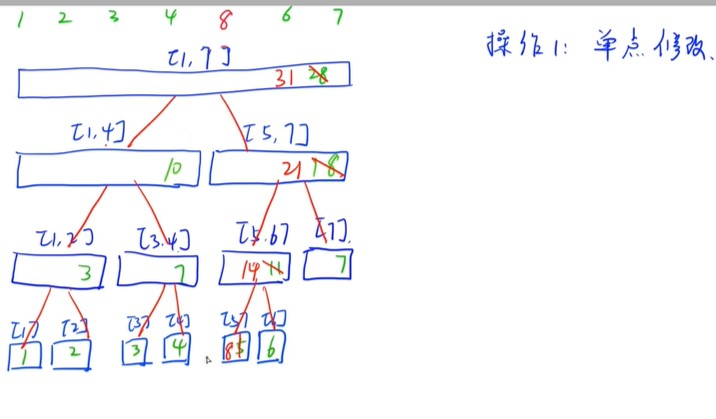
  • 区间查询（Ologn）

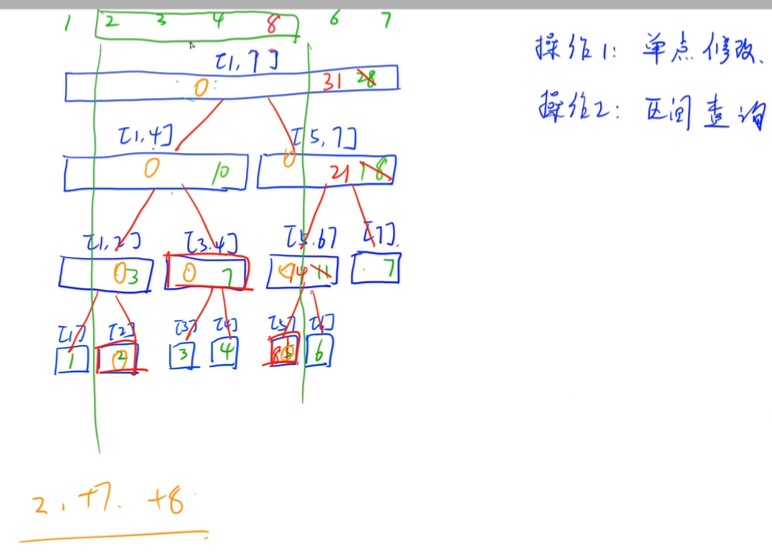
  • 染色求面积求长度

  • pushup：用子节点信息更新当前节点信息
  • build：在一段区间上初始化线段树
  • modify：修改
  • query：查询

1
#include

STL简介

详情看备战408（1）

当系统为某一个程序分配空间的时候，所需的时间基本上与空间大小无关，与申请次数有关，比如申请一个长度为1000的数组和申请1000个长度为1的数组，因此vector的思路是可以浪费空间但要减少申请次数，如先申请32，再申请64，不够的时候将长度*2，因此要申请一个长度为n的数组，申请空间次数是logn，额外copy的次数大概是O1

vector

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector, 变长数组，倍增的思想
    size()  返回元素个数//a.size() O(1)
    empty()  返回是否为空//a.empty() O(1)
    clear()  清空//a.clear()
    front()/back()
    push_back()/pop_back()
    begin()/end()//end是末尾的下一个位置，a[0]和a[a.size()]
    []//支持随机选址
    支持比较运算，按字典序
    
例：
    vector<int>a(10);//定义一个长度为10的vector
	vector<int>a(10,3);//定义一个长度为10，里面全部为3的vector
	for(auto x:a)	cout<<x<<endl;//遍历一遍vector

pair

1
2
3
4
5
6
7
pair<int, int>
    first, 第一个元素
    second, 第二个元素
    支持比较运算，以first为第一关键字，以second为第二关键字（字典序）
    p=make_pair(10,"kugeln");
	p = {20,"abc"};//C++11用法
//当一个东西有两个不同的属性，可以用pair来存，如果要按照某个属性排序，可以把排序关键字放在first，不需要排序的放在second，然后对整个pair排序，如果有三种属性,可以用pair<int,pair<int,int>>p来存

string

1
2
3
4
5
6
string，字符串
    size()/length()  返回字符串长度
    empty()
    clear()
    substr(起始下标，(子串长度))  返回子串，超过数组长度就输出到最后一个字符为止
    c_str()  返回字符串所在字符数组的起始地址

queue

1
2
3
4
5
6
7
8
9
10
queue, 队列
    size()
    empty()
    push()  向队尾插入一个元素
    front()  返回队头元素
    back()  返回队尾元素
    pop()  弹出队头元素
    //没有clear函数
    //清空队列，即重新初始化
    q = queue<int> ();

priority_queue

1
2
3
4
5
6
7
8
priority_queue, 优先队列，默认是大根堆
    size()
    empty()
    push()  插入一个元素
    top()  返回堆顶元素
    pop()  弹出堆顶元素
    定义成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;
//或者直接插入负数 heap.push(-x);

stack

1
2
3
4
5
6
7
stack, 栈
    size()
    empty()
    push()  向栈顶插入一个元素
    top()  返回栈顶元素
    pop()  弹出栈顶元素
//没有clear函数

deque

1
2
3
4
5
6
7
8
9
deque, 双端队列//相当于加强版vector
    size()
    empty()
    clear()
    front()/back()
    push_back()/pop_back()
    push_front()/pop_front()
    begin()/end()
    []//支持随机选址

set,map,multiset,multimap

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
set, map, multiset, multimap, 基于平衡二叉树（红黑树），动态维护有序序列
    size()
    empty()
    clear()
    begin()/end()
    ++, -- 返回前驱和后继，时间复杂度 O(logn)

    set/multiset//set不能有重复元素，multiset可以有重复元素
        insert()  插入一个数
        find()  查找一个数
        count()  返回某一个数的个数
        erase()
            (1) 输入是一个数x，删除所有x   O(k + logn)
            (2) 输入一个迭代器，删除这个迭代器
        lower_bound()/upper_bound()
            lower_bound(x)  返回大于等于x的最小的数的迭代器
            upper_bound(x)  返回大于x的最小的数的迭代器
    
    map/multimap
        insert()  插入的数是一个pair
        erase()  输入的参数是pair或者迭代器
        find()
        []  注意multimap不支持此操作。 时间复杂度是 O(logn)
        lower_bound()/upper_bound()
		
    
    
unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表
    和上面类似，增删改查的时间复杂度是 O(1)
    不支持 lower_bound()/upper_bound()， 迭代器的++，--，因为内部是无序的，所以和排序有关的所有操作都没法用

bitset

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bitset, 圧位//比如说1024个bool数组要1024个字节，但是bool数组由0和1组成，可以将0和1压到每一个字节中，相当于一个字节存8个0或者1，只需要128个字节
    //想要存储一个大的bool矩阵，但是超过了题目大小限制，可以通过bitset压位到1/8
    bitset<10000> s;//<>里面写的个数
    ~, &, |, ^//取反，与，或，异或
    >>, <<
    ==, !=
    []

    count()  返回有多少个1

    any()  判断是否至少有一个1
    none()  判断是否全为0

    set()  把所有位置成1
    set(k, v)  将第k位变成v
    reset()  把所有位变成0
    flip()  等价于~
    flip(k) 把第k位取反
算法
#算法
算法·基础算法与数据结构
http://example.com/2024/03/22/备战408（2）/
作者
Kugeln
发布于
2024年3月22日
许可协议