数据结构算法笔试

如何备考数据结构大题

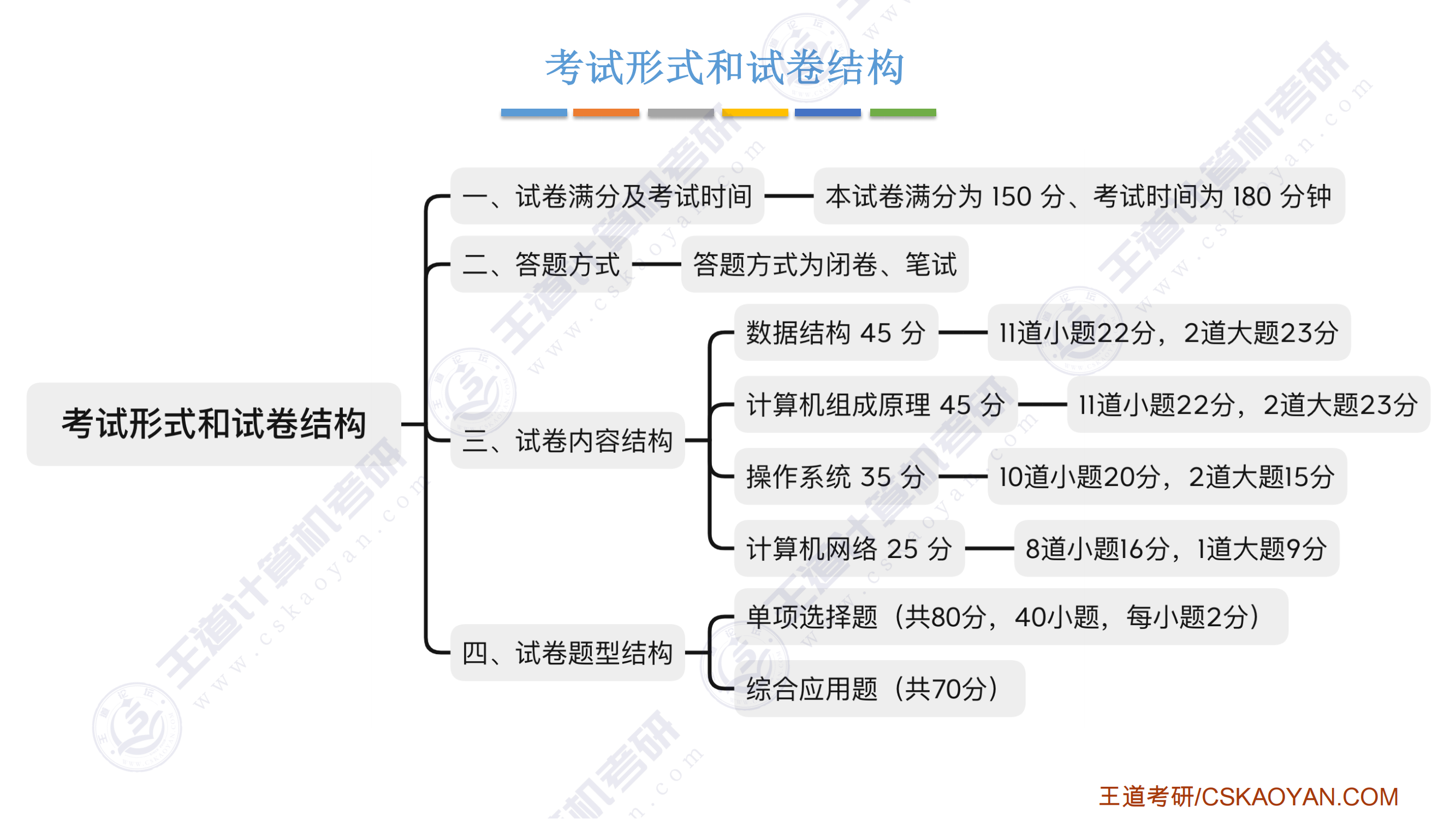
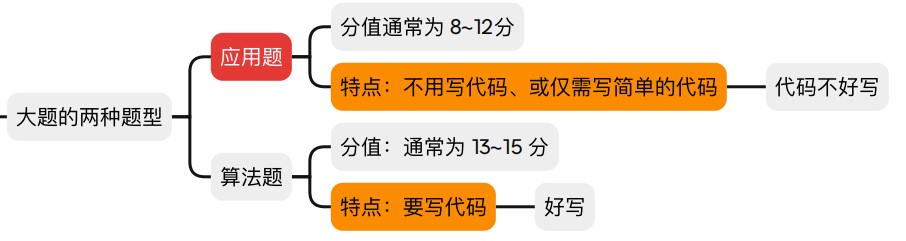
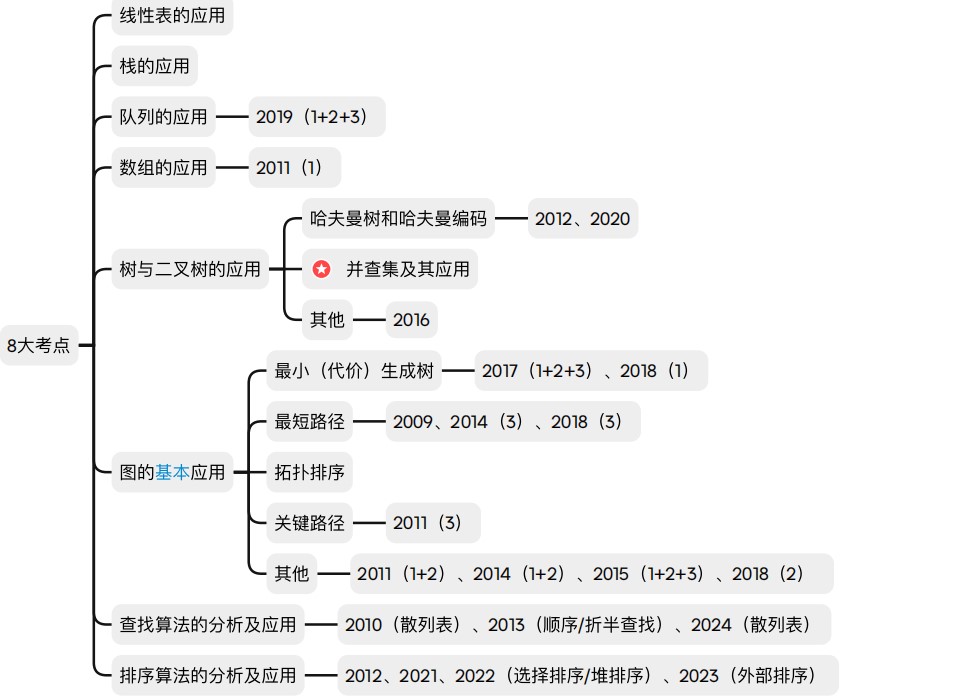
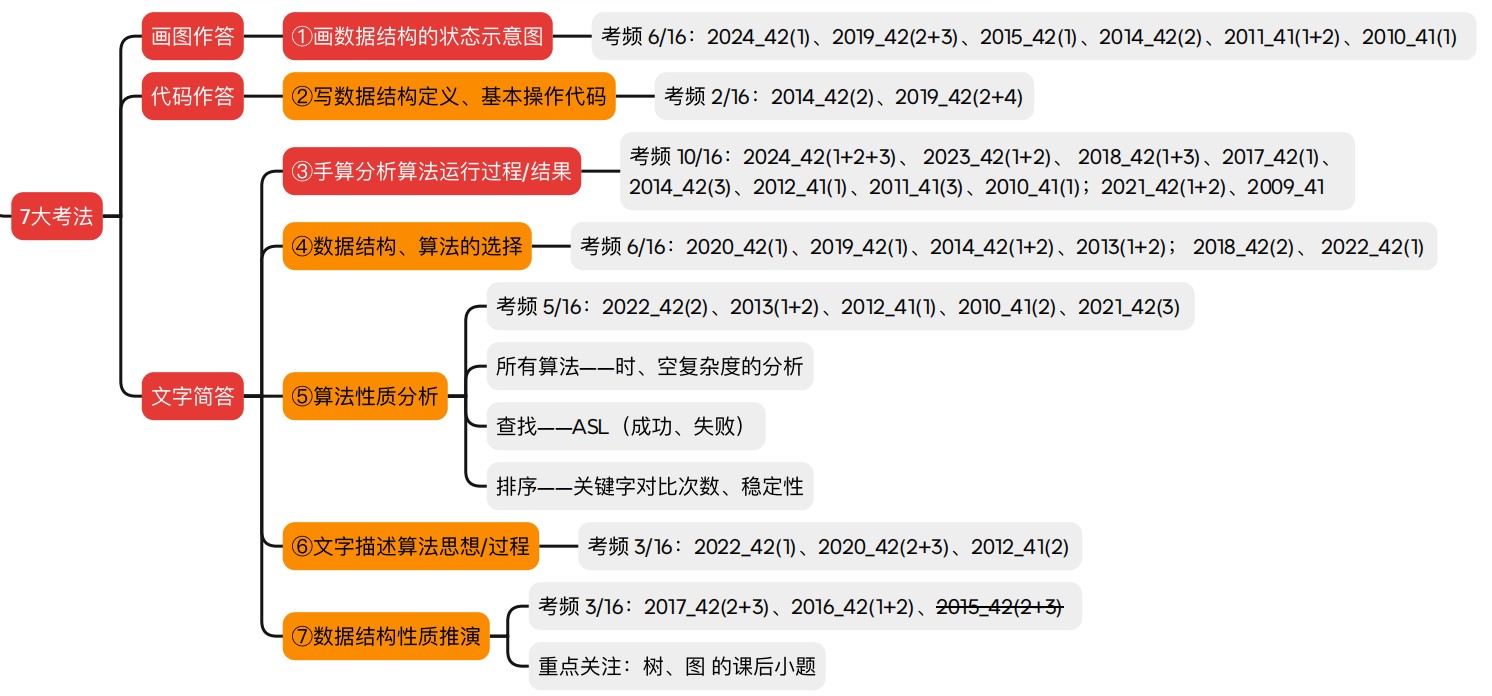
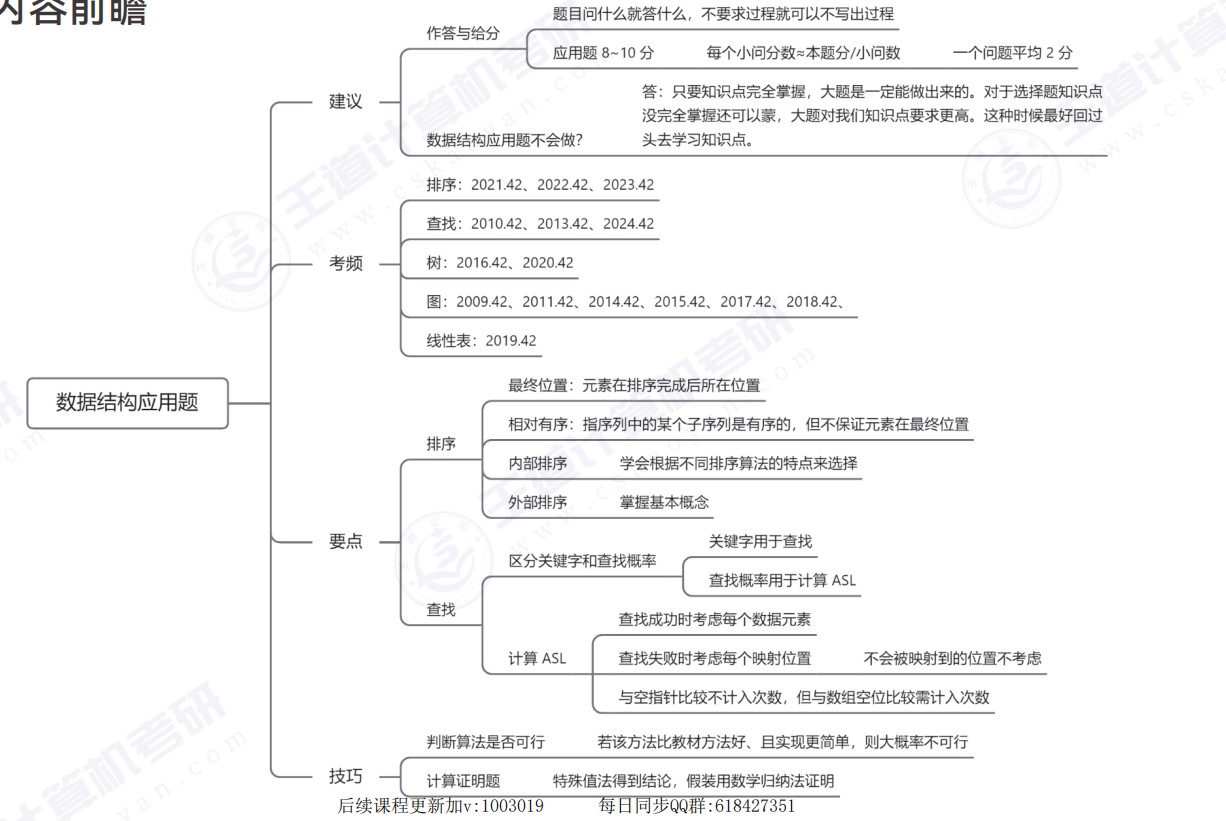
  • 数据结构的小题最好的复习方法是把王道书的课后习题二刷
  • 多做题少听课
  • 主动发现自己不足的地方，去查缺补漏而不是遍历课本

大题的题型

  • 应用题侧重于算法的逻辑而不是算法代码的实现
  • 大纲里面应用相关即大题要考的考点
  • 应用题备考思路：
    • 画数据结构和算法运行过程
    • 训练数据结构定义的简单代码
    • 基本操作的简单代码

八大考点

①线性表的应用

②栈的应用

③队列的应用

④数组的应用

⑤树与二叉树的应用

  • 二叉树基本考的就是哈夫曼树和哈夫曼编码，并查集及其应用。其他的题型通常是定义数据结构或者实现基本操作

⑥图的基本应用

  • 比较基本的应用
  • 应用题一般不用写代码但是要手算，能够懂这些算法运行的逻辑
最小（代价）生成树
  • 最小生成树考察的是一个图中包含多个点的总路线代价最短
    • 而单源最短路径只考虑两点之间最短距离的路径
最短路径
拓扑排序
关键路径
其他
  • 数据结构定义
  • 画图

⑦查找算法的分析及应用

  • 二叉搜索树、平衡二叉树和红黑树可能和树与二叉树考点进行比较深度的结合

    • 比如给出一个关键字序列，从一个空的二叉树开始插入这些关键字，然后画出插入以后的平衡二叉树的形态，同时给出这个平衡二叉树的数据结构定义
    • 大概率应用题而不是代码
    • 尤其是平衡二叉树和红黑树

  • 散列（哈希）表

    • 大概率应用题而不是代码

  • B树及其基本操作

    • 不太可能在应用题当中考察，只考基本概念，不用管基本操作，b树小题里面一般可能考

  • 分块查找

    • 应用题

  • 字符串模式匹配

    • 大概率应用题而不是代码

  • 查找算法的性能分析，分析平均查找长度，成功的ASL和失败的ASL

⑧排序算法的分析及应用

  • 希尔排序
    • 更容易考小题而不是应用题
  • 堆排序
  • 基数排序
  • 外部排序

七大考法

①画图作答

  • （1）画数据结构的状态示意图
    • 重中之重
    • 一般是考察比较复杂的数据结构的图示

②代码作答

  • （1）写数据结构定义、基本操作代码
    • 简单的代码
    • 基本操作/功能的代码片段，比如判断队空或者插入
    • 比较复杂的数据结构不会考很复杂的算法题，但可能考数据结构的代码定义以及基本操作的代码实现

③文字简答

  • （1）手算分析算法运行过程/结果
  • （2）数据结构、算法的选择
    • 基于应用场景选择一种合适的数据结构
    • 基于应用场景选择一种性能比较好的算法
  • （3）算法性质分析
    • 分析算法的时间复杂度和空间复杂度
      • 所有算法都有可能考
    • 查找算法
      • 分析平均查找长度
      • 成功ASL和失败ASL
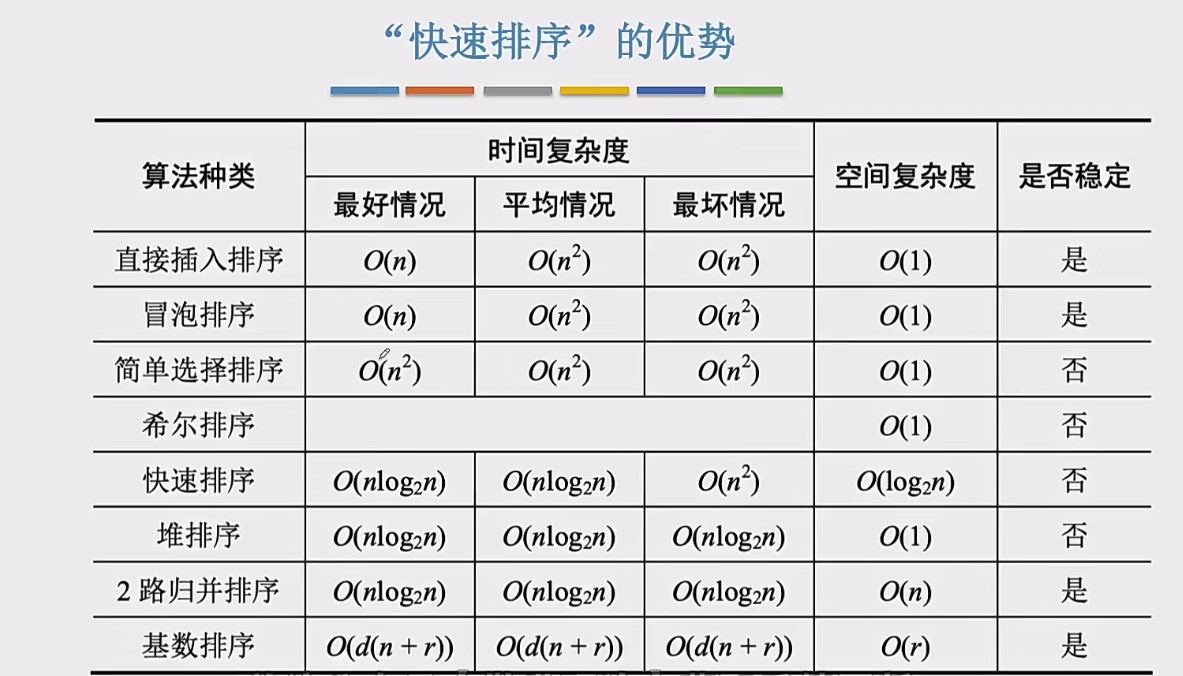
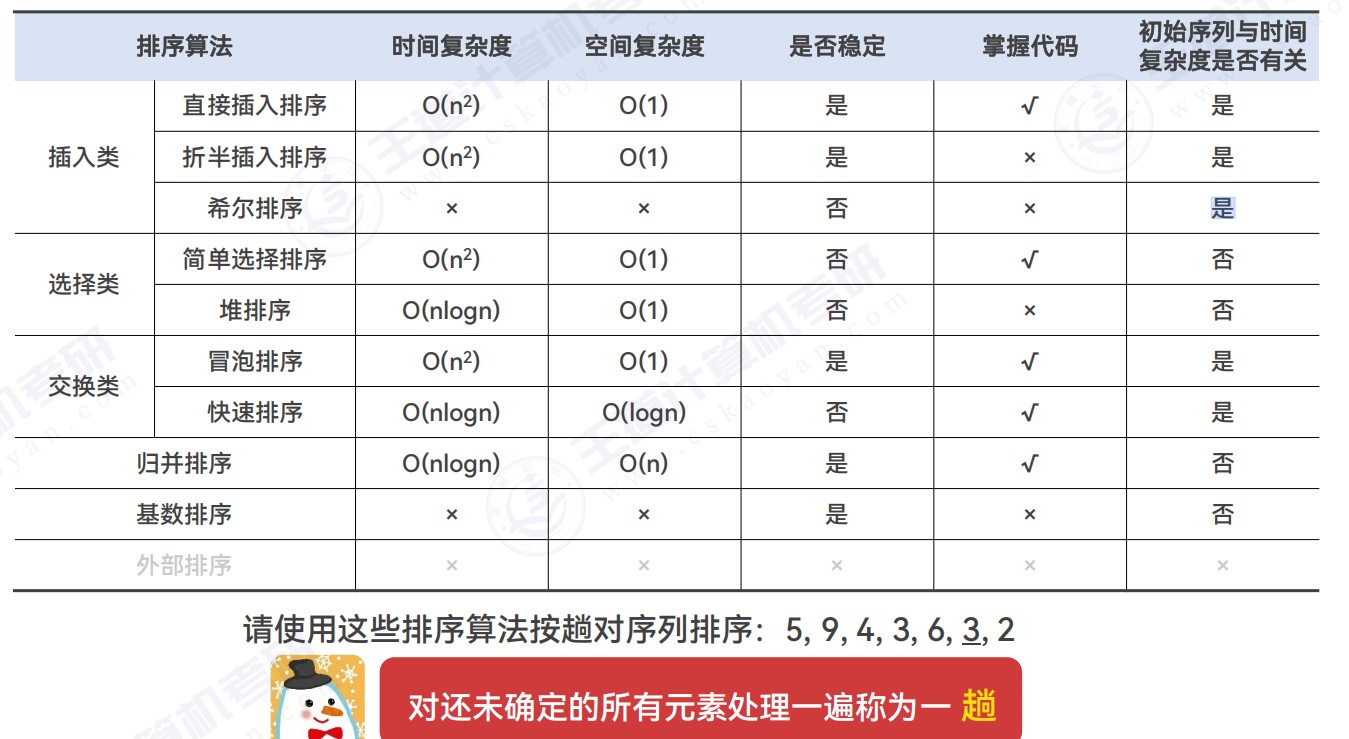
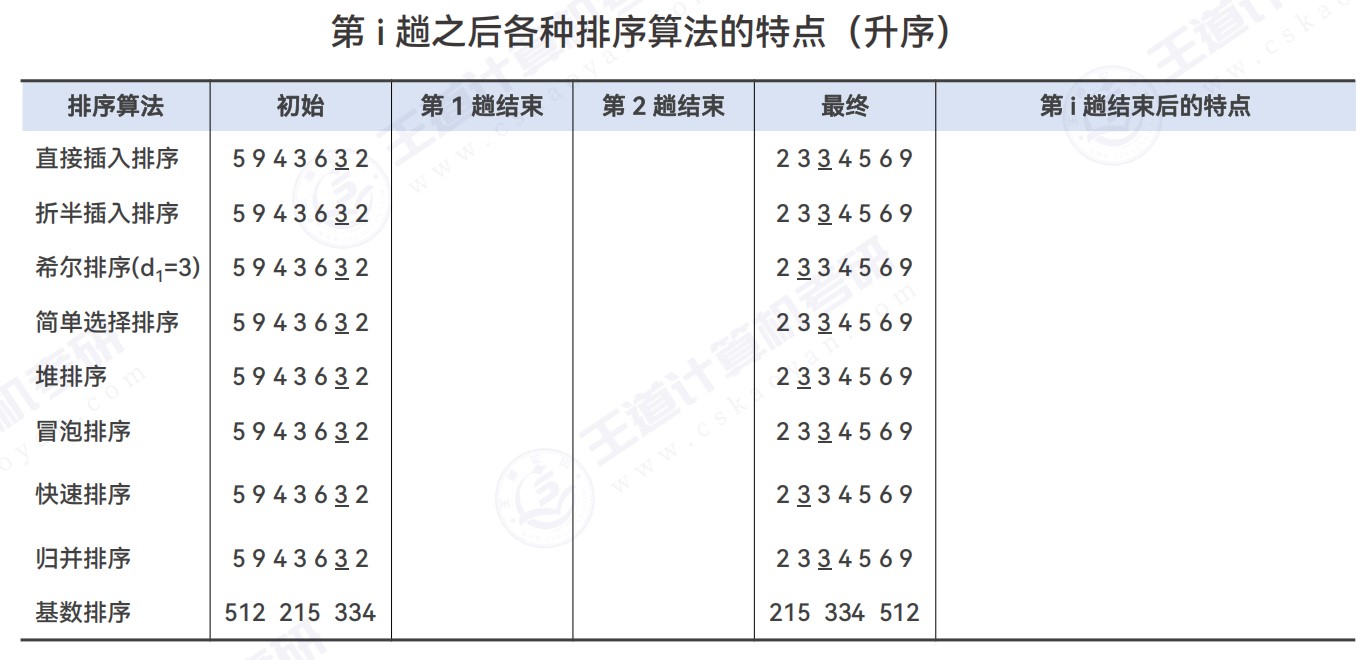
    • 排序算法
      • 分析关键字的对比次数
        • 某一趟排序当中关键字的对比次数是多少
        • 排完序关键字的总对比次数是多少
      • 稳定性
  • （4）文字描述算法思想/过程
    • 可以通过示意图去解释算法的运行过程，用文字描述也可以解和画图去做
    • 将画数据结构的状态示意图和手算分析算法运行过程/结果结合起来，从这两个角度去把各个算法的运行过程和数据结构的示意图捋清楚
  • （5）数据结构性质推演
    • 树和图的性质推演
      • 主要根据王道书的课后小题来复习

应用题

  • 先找到题目中的线索，然后遍历一下这类问题的做法

排序类应用题

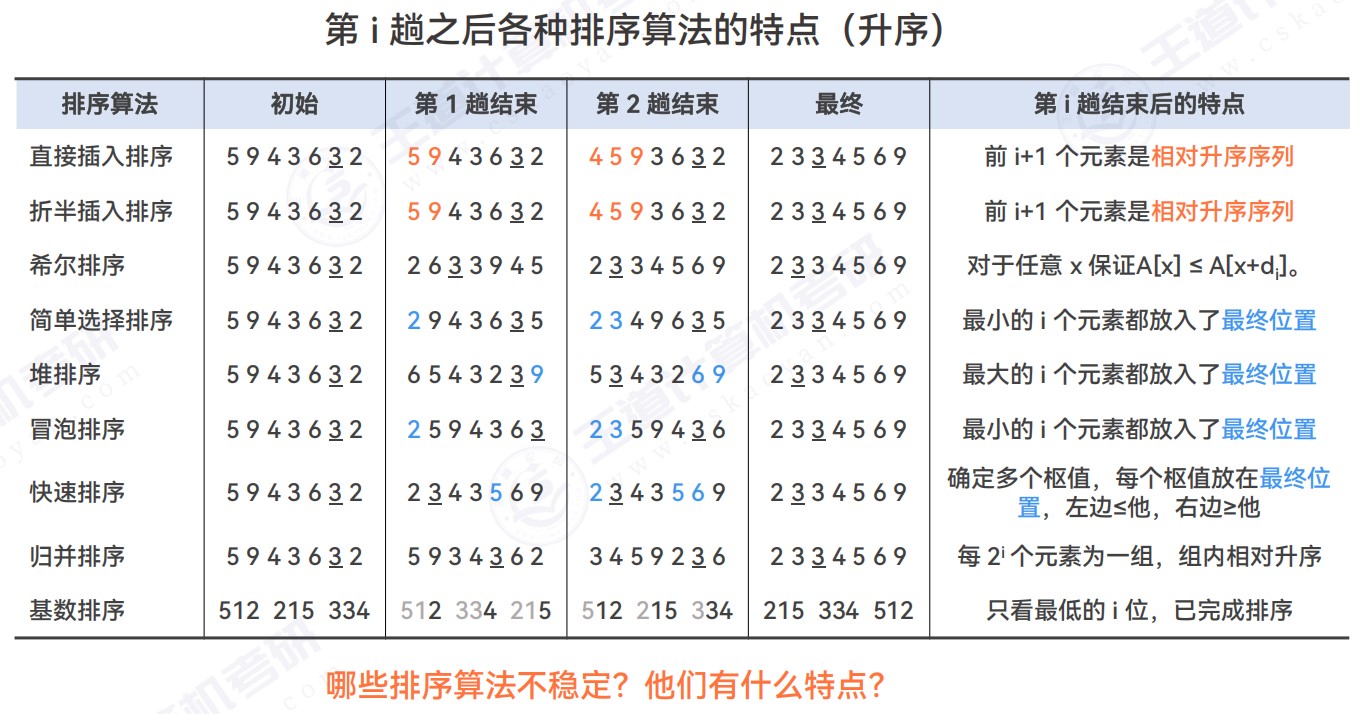
  • 插入类排序：直接插入排序、折半插入排序、希尔排序
    • 能够保证相对升序的序列（有可能是跳跃的，也有可能是前面的i+1个
  • 选择类排序：简单选择排序、堆排序
    • 堆排序：（大根堆）每次选择堆顶元素放在最后（和堆底元素交换），每次将最大的元素放在最后面
      • 第一趟排序是先顺序存进一个二叉树，调整成为一个大根堆，再把它那个最大的元素换到最后面，再次调整为大根堆的结果
    • 每次都有一个元素被放在最终位置
  • 交换类排序：冒泡排序、快速排序
    • 每次根据逆序对进行交换
    • 快速排序：
      • 枢值一般选取序列的第一个元素
  • 不稳定排序算法的特点
    • 对于一种排序算法，我们要交换前两个位置的时候，如果它看不到前面有一个和他相同的元素，就有可能出现不稳定

查找类应用题

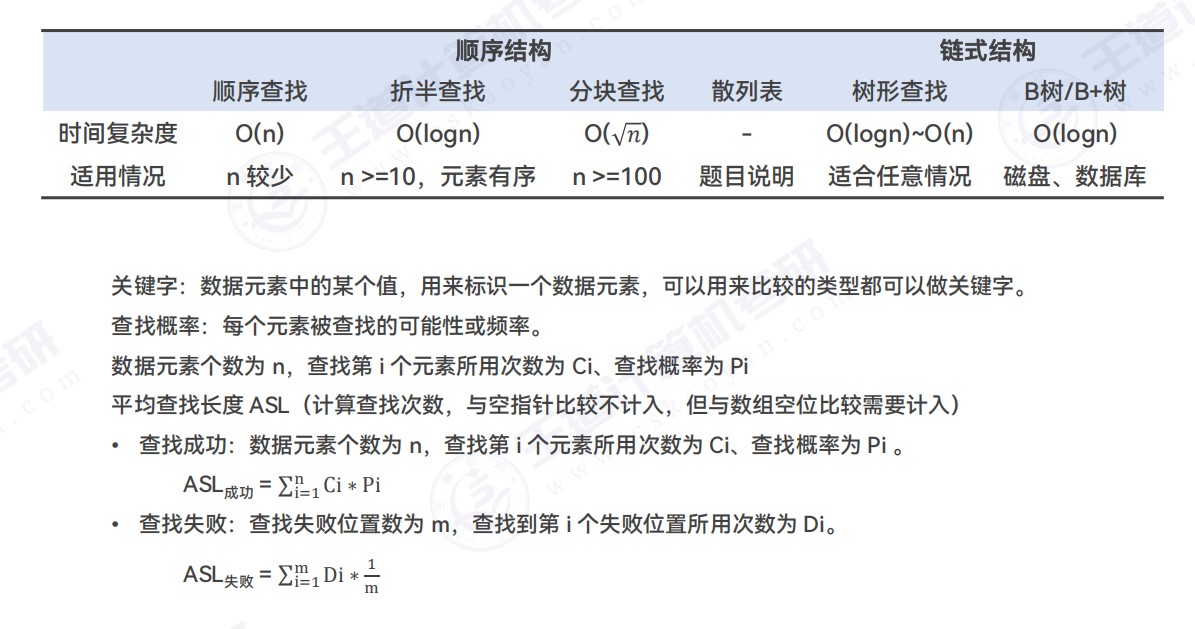
  • 折半查找
    • 元素有序，顺序表
  • 散列查找查找失败的情况
    • 线性探测法，查找到空位的时候说明查找失败，比较空的数组元素会计入一次比较次数
    • 链地址法，比较到一个空指针的位置才是查找失败，但是该比较空指针不会算进比较次数
    • 装填因子在链地址法中可以大于1，但是存储效率一定是小于等于100%的
    • 查找成功的时候分母是元素数量，查找失败的时候分母是取模后面的那个数字（因为无法映射到其他更大的数字）

  • 链式存储，考虑二叉搜索树
  • 顺序存储，顺序查找和折半查找（注意排序）比较常见

树类应用题

图类应用题

线性表类应用题

算法题

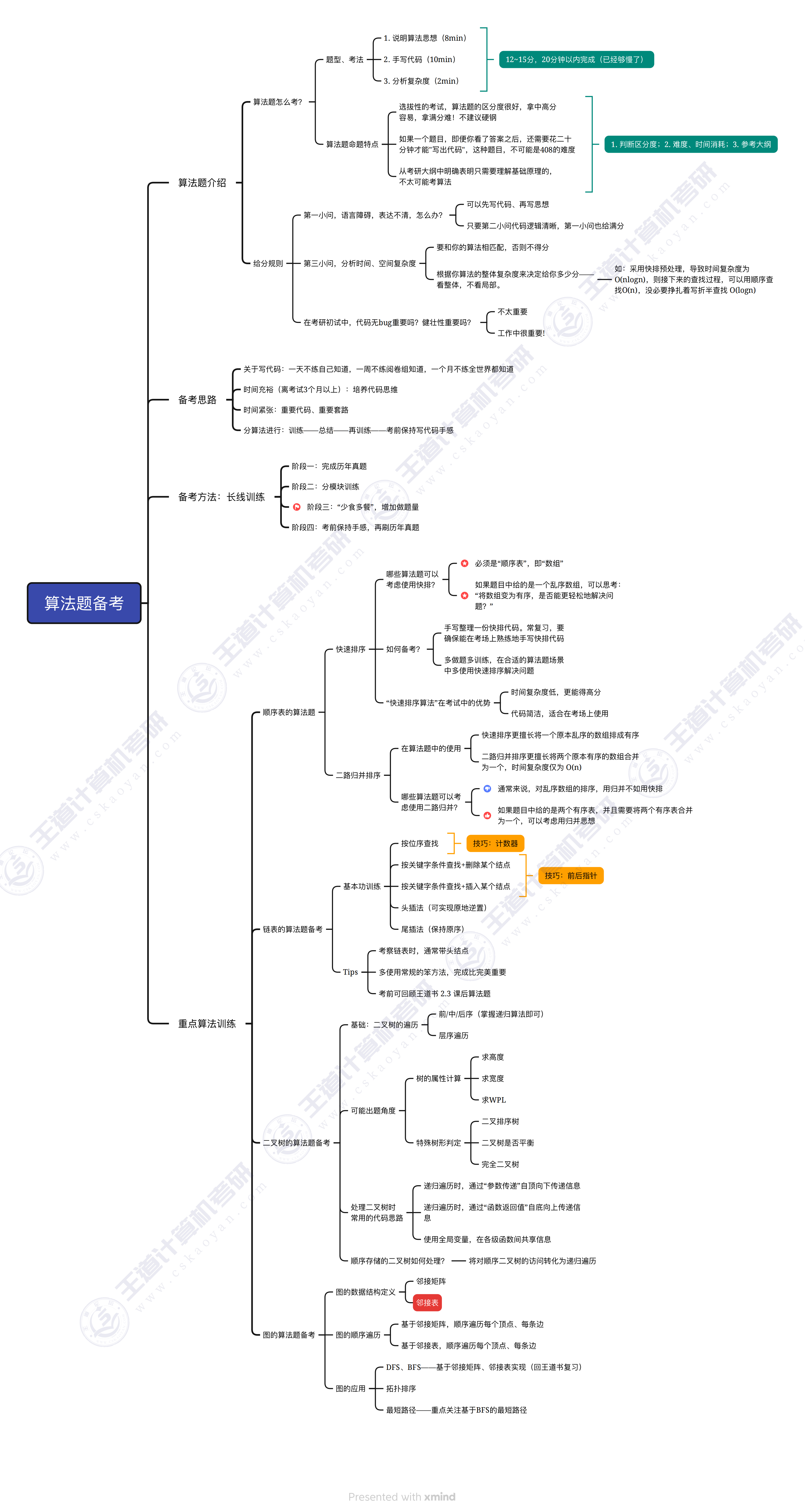
  • 算法题
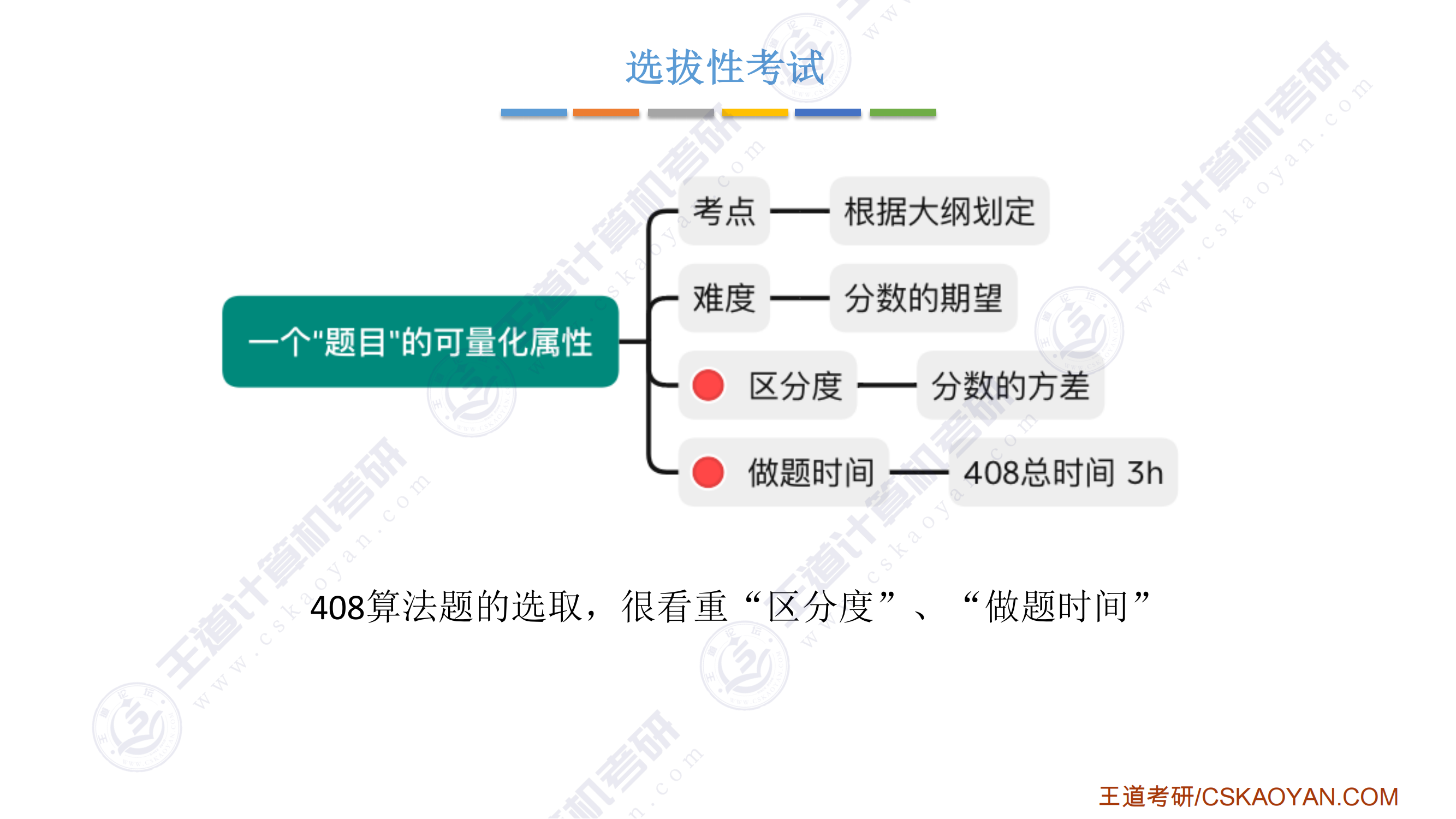
    • 一题多解，分数高中低三档
    • 可以先写第二小问再写第一小问
    • 顺序表和链表一般情况下要考察时间复杂度
    • 树和图一般不考时间复杂度和空间复杂度，分析要求低一点，但依旧要记得
      • 树和图能解决问题比高效解决问题最重要，只要能解决问题笨方法也可以，只要能掌握常规代码即可
  • 备考方法
    • 阶段一：完成历年真题
    • 阶段二：分模块训练
    • 阶段三：少食多餐，增加做题量
    • 阶段四：考前保持手感，再刷历年真题

排序

顺序表

  • 快排和堆排是所有排序算法中效率最高的，但是快排代码简单，堆排代码复杂，所以快排最优

  • 考试按照时间复杂度给分

    • 通常来说，408算法题不会限制具体使用哪种算法
    • 408算法题通常按照复杂度给分，复杂度越低，给分越高
    • 若题目没有特别要求，答题时回答“平均复杂度”即可

  • 套路型算法：

    • 快速排序
      • 能快排就快排，不能用快排的再考虑用其他排序
      • 快排只能在顺序表和数组（静态链表）中使用，链表当中不能用快排，因此当涉及顺序表（数组）的题目，考虑能否使用到快速排序。
      • 如果题目中给的是一个乱序数组的话，如果把这个乱序数组变成有序，我们用快排的套路，先把它变成有序，能否更加轻松的解决这个问题，从这个角度思考
      • 时间复杂度O(nlogn)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    void quick_sort(int q[], int l, int r)
    {
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
     while (i < j)
       {
            do i ++ ; while (q[i] < x);
            do j -- ; while (q[j] > x);
            if (i < j) swap(q[i], q[j]);
       }
        quick_sort(q, l, j), quick_sort(q, j + 1, r);
    }
    C++
    • 归并排序
      • 时间复杂度O(nlogn)
      • 如果我们在考题当中遇到排序类的题目，要求把一个乱序的数组排成一个更大的数组，如果这个数组本身部分有序，那么我们采用归并排序比快速排序更加优秀
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    void merge_sort(int q[], int l, int r)
    {
        if (l >= r) return;

        int mid = l + r >> 1;
        merge_sort(q, l, mid);
        merge_sort(q, mid + 1, r);

        int k = 0, i = l, j = mid + 1;
        while (i <= mid && j <= r)
            if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
            else tmp[k ++ ] = q[j ++ ];

        while (i <= mid) tmp[k ++ ] = q[i ++ ];
        while (j <= r) tmp[k ++ ] = q[j ++ ];

        for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];

    }
    C++
    • 快速排序更擅长将一个原本乱序的数组排成有序
      • 二路归并排序更擅长将两个原本有序的数组合并为一个，时间复杂度仅为O(n)
      • 通常来说，对乱序数组的排序，用归并不如用快排
      • 如果题目中给的是两个有序表，并且需要将两个有序表合并为一个，可以考虑用归并思想

链表

  • 不支持随机访问，算法较少
  • 考察偏向于考基本功
    • 按位序查找
    • 按关键字条件查找+删除某个节点
    • 按关键字条件查找+插入某个节点
    • 头插法（可实现原地逆置）
    • 尾插法（保持原序）

树

  • 掌握前中后序遍历、层序遍历、递归算法
    • 非递归算法不用掌握
    • 基于这些算法解决思维导图中列出的问题，然后做一下王道书的剩余算法题

图

  • 数据结构层面

    • 邻接矩阵和邻接表的遍历
      • 邻接矩阵可以for循环遍历
    • 但是邻接表只能bfs或者dfs
    • 邻接多重表和十字链表的定义

  • 算法备考

    • 栈、队列的数组表示（用来理解下面的代码）
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    // tt表示栈顶
    int stk[N], tt = 0;//stk表示栈，tt表示栈顶下标

    // 向栈顶插入一个数
    stk[ ++ tt] = x;

    // 从栈顶弹出一个数
    tt -- ;

    // 栈顶的值
    stk[tt];

    C++

// 判断栈是否为空，如果 tt > 0，则表示不为空
if (tt > 0) not empty;
else empty;

//栈顶
stk[tt];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

```c++
// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

//取出队尾
q[tt];

// 判断队列是否为空，如果 hh <= tt，则表示不为空
if (hh <= tt) not empty;
    else empty;

PHP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
  //循环队列
  // hh 表示队头，tt表示队尾的后一个位置
  int q[N], hh = 0, tt = 0;
  
  // 向队尾插入一个数
  q[tt ++ ] = x;
  if (tt == N) tt = 0;
  
  // 从队头弹出一个数
  hh ++ ;
  if (hh == N) hh = 0;
  
// 队头的值
  q[hh];

  // 判断队列是否为空，如果hh != tt，则表示不为空
if (hh != tt)
  {
  
  }
  
C++
  • DFS，BFS
1
2
3
4
5
6
7
8
9
10
11
bool st[N];
int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])//遍历点的边
    {
        int j = e[i];//存储当前链表节点对应的图里面的点的编号
        if (!st[j]) dfs(j);//j没有被搜到，继续搜
    }
}
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
queue<int> q;//初始化
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())//队列不空
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
      {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

int bfs()
{
	int hh =0,tt=0;//定义队头队尾
    q[0]=1;//q的第一个元素起点
    memset(d,-1,sizeof d);//初始化距离，-1表示没有被遍历过
    d[1]=0;//第一个点遍历
    while(hh<=tt){//队列不空
        int t=q[hh++]//取到队头
            for(int i = h[t];i!=-1;i=e[i])//拓展队头
            {
                int j =e[i];//拓展到队头连接的下一个点
               if(d[j]==-1)//d[j]没有被拓展过
               {
                   d[j]=d[t]+1;
                   q[++tt]=j;
               }
            }
    }
    return 0;
}
C++
  • 拓扑排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int n,m;
int h[N],e[N],ne[N],idx;
int d[N],q[N];//d[n]表示入度，q[n]是拓扑序列
void add(int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a]=idx++;
    
}
bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;//数组模拟入队

    while (hh <= tt)//队列不空
    {
        int t = q[hh ++ ];//取出来队头

        for (int i = h[t]; i != -1; i = ne[i])//枚举t的所有出边t->j，删掉t->j
        {
            int j = e[i];//找到出边
           d[j]--;
            if ( d[j] == 0)//前面的所有点都已经排好了
                q[ ++ tt] = j;//j入队
         
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}
//出队的顺序就是拓扑序
C++

一休的算法题建议

评分细则

  • 顺序表、链表注意复杂度
    • 分数差别主要在于时间复杂度
  • 树、图注意细节
    • 分数差别主要在于特殊情况是否考虑到
  • 序列就是数组

答题技巧

  • 顺序表和链表

    • 暴力解
      • 枚举
    • 其他解
      • 有序
        • 折半查找
          • 链表不适用
          • 适用于有序数组
        • 多指针法（归并思想）
      • 无序
        • 散列表
          • 典型应用：计数器
        • 先排序再按有序做
        • 快排思想
    • 目标：尽量优化自己的算法，让自己的复杂度变低

  • 树

    • 核心是遍历（递归）
      • 先序
      • 中序
      • 后序
      • 层序
    • 实际上王道书上的树的递归算法可以跳过，因为不同的先序、后序、中序算法都是不一样的，还有不一样的写法。
      • 如果递归的话，先中后逻辑都是一样的，实际上只有三行核心代码
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    //先序（根→左→右）
    void preorder(btnode *p){
        if(p==NULL){
            return;
            visit(p);//对p结点访问等，这道题真正要写的东西，比如题目要求我们做什么，树的每道题不同的点就在于这个visit
            preorder(p->lchild);
            preorder(p->rchild);
            //这三条语句，visit在先就是先序，在中就是中序，在后就是后序
        }
    }
    //中序（左→根→右）
    void inorder(btnode *p){
        if(p==NULL)
            return ;
       inorder(p->lchild);
        visit(p);
        inorder(p->rchild);
    }
    //后序（左→右→根）
    void postorder(btnode *p){
        if(p==NULL)
            return;
        postorder(p->lchild);
        postorder(p->rchild);
        visit(p);
    }
    C++

  • 图

    • 基本遍历
    • 最小生成树
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    //普利姆prim算法,时间复杂度O(n^2)
    int n;      // n表示点数
    int g[N][N];        // 邻接矩阵，存储所有边
    int dist[N];        // 存储其他点到当前最小生成树的距离
    bool st[N];     // 存储每个点是否已经在生成树中

    //到集合的距离就是一个点连接集合的所有边中最短的那一条
    // 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
    int prim()
    {
        memset(dist, 0x3f, sizeof dist);//初始化最短距离

        int res = 0;
        for (int i = 0; i < n; i ++ )//n次迭代
        {
            int t = -1;//不在集合当中的距离最小点的编号
            for (int j = 1; j <= n; j ++ )
                if (!st[j] && (t == -1 || dist[t] > dist[j]))
                    t = j;

            if (i && dist[t] == INF) return INF;

            if (i) res += dist[t];//只要不是第一个点
            st[t] = true;

            for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
        }

        return res;
    }
    C++
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    //克鲁斯卡尔Kruskal算法,时间复杂度O(mlogn)
    int n, m;       // n是点数，m是边数
    int p[N];       // 并查集的父节点数组

    struct Edge     // 存储边
    {
        int a, b, w;

        bool operator< (const Edge &W)const//重载小于号
        {
            return w < W.w;
        }
    }edges[M];

    int find(int x)     // 并查集核心操作
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    int kruskal()
    {
        sort(edges, edges + m);//把所有边排序

        for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

        int res = 0, cnt = 0;
        for (int i = 0; i < m; i ++ )//从小到大枚举所有边
        {
            int a = edges[i].a, b = edges[i].b, w = edges[i].w;

            a = find(a), b = find(b);//让a，b分别等于祖宗节点
            if (a != b)     // 如果两个连通块不连通，则将这两个连通块合并
            {
                p[a] = b;//合并两个连通块
                res += w;//存的是最小生成树中所有树边的权重之和
                cnt ++ ;//存的是当前加入了多时少条边
            }
        }

        if (cnt < n - 1) return INF;//图不是联通的
        return res;//输出所有树边的权重之和
    }
    C++
    • 最短路径
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    //朴素dijkstra算法，时间复杂度O(n^2)
    int g[N][N];  // 存储每条边
    int dist[N];  // 存储1号点到每个点的最短距离
    bool st[N];   // 存储每个点的最短路是否已经确定

    // 求1号点到n号点的最短路，如果不存在则返回-1
    int dijkstra()
    {
        memset(dist, 0x3f, sizeof dist);//初始化其他距离
        dist[1] = 0;//初始化第一个点的距离

        for (int i = 0; i < n - 1; i ++ )
        {
            int t = -1;     // 在还未确定最短路的点中，寻找距离最小的点
            for (int j = 1; j <= n; j ++ )
                if (!st[j] && (t == -1 || dist[t] > dist[j]))//当前点还没有确定最短路；没有赋值或者不是最短的
                    t = j;//赋值
      // if(t==n)break;//优化可以加上
            // 用t更新其他点的距离
            for (int j = 1; j <= n; j ++ )
                dist[j] = min(dist[j], dist[t] + g[t][j]);
    //判断长度，得出最小距离并更新
            st[t] = true;
        }

        if (dist[n] == 0x3f3f3f3f) //不连通
            return -1;
        return dist[n];
    }
    //输入输出
    cin >> n>>m;
    memset(g,0x3f,sizeof g);
    while(m--){
        int a,b,c;
        cin>>a>>b>>c;
        g[a][b]=min(g[a][b],c);
    }
    int t =dijkstra()l
        cout<<t;
    return 0;
    C++
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    //堆优化版dijkstra算法，时间复杂度O(mlogn)
    typedef pair<int, int> PII;

    int n;      // 点的数量
    int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
    int dist[N];        // 存储所有点到1号点的距离
    bool st[N];     // 存储每个点的最短距离是否已确定

    void add(int a,int b,int c){
        e[idx]=b,w[idx]= c,ne[idx]=h[a],h[a]=idx++;
    }
    // 求1号点到n号点的最短距离，如果不存在，则返回-1
    int dijkstra()
    {
        memset(dist, 0x3f, sizeof dist);
        dist[1] = 0;
        priority_queue<PII, vector<PII>, greater<PII>> heap;//定义小根堆
        heap.push({0, 1});      // first存储距离，second存储节点编号

        while (heap.size())//堆里面非空
        {
            auto t = heap.top();
            heap.pop();

            int ver = t.second, distance = t.first;//编号；距离

            if (st[ver]) continue;//冗余备份
            st[ver] = true;

            for (int i = h[ver]; i != -1; i = ne[i])
            {
                int j = e[i];
                if (dist[j] > distance + w[i])
                {
                    dist[j] = distance + w[i];//更新距离
                    heap.push({dist[j], j});//放入堆
                }
            }
        }

        if (dist[n] == 0x3f3f3f3f) return -1;
        return dist[n];
    }
    int main(){
        cin >> n>>m;
        memset(h,-1,sizeof h);
        while(m--){
            int a,b,c;
            cin >> a >> b>>c;
            add(a,b,c);
        }
        int t = dijkstra();
        cout<<t;
        return 0;
    }
    C++
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    //Floyd算法,时间复杂度O(n^3)
    cosnt int INF=1e9;
    初始化：
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                if (i == j) d[i][j] = 0;
                else d[i][j] = INF;

    // 算法结束后，d[a][b]表示a到b的最短距离
    void floyd()
    {
        for (int k = 1; k <= n; k ++ )
            for (int i = 1; i <= n; i ++ )
                for (int j = 1; j <= n; j ++ )
                    d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
    }

    C++
    • 拓扑排序
    • 关键路径
    • 目标：考虑一些细节是否到位

  • 能不能直接调用函数

    • 5行以下的随便调用
    1
    2
    3
    4
    5
    6
    pop();
    push();
    swap(a,b);
    abs();
    pow(x,y);//x的y次幂
    sqrt();//平方根
    C++

  • 过程

    • 考前最好复习一遍常用的算法模板
1
2
3
4
5
6
7
8
//先假设所用函数已经设立，然后在主函数那里直接用，用完再回去写该函数
//如假如要用折半查找，先
int binary(){
//先留空，下面的ans函数写完再回来写
}
int ans(int s[],int n ,int k){
//答案
}
C++
  • 空间复杂度的分析
    • 申请了哪些数组
    • 申请了哪些结点
    • 递归的时候有多少层的递归（树的高度，递归的层数）

栈、队列的一些代码模板

数组实现栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//数组实现栈

//初始化栈
int stk[N],tt=0;
//入栈
stk[++tt]=x;
//弹出栈顶元素但是不出栈
x=stk[tt];
//弹出栈顶元素并且出栈
x=stk[tt--];
//判断栈空
if(tt==0)
//判断栈满
if(tt==maxsize)
C++

链表实现栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//链表实现栈

//定义栈结点
struct Lnode{
    int data;
    Lnode* next;
};
using listack=Lnode*;
//初始化链表实现栈
bool initstack(listack &s){
  s=new Lnode;
    s->next=nullptr;
    return true;
}
//栈空
bool isempty(listack s){
    if(s->next==nullptr)
        return true;
    else 
        return false;
    
    
}
//入栈
bool push(listack &s,int x){
    Lnode *p=new Lnode;
    p->data= x;
    p->next=s->next;
    s->next=p;
    return true;
}
//出栈
bool pop(listack &s,int &x){
    if(isempty(s)) return false;
    Lnode *p=s->next;
    x=p->data;
    s->next=p->next;
    delete p;
    return true;
}

C++

双向链表实现栈（栈顶在链尾）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//双链表实现栈，栈顶在链尾

//定义双链表结点
struct dnode{
    int data;
    dnode*pre,*next;
};
//定义栈
struct dstack{
    dnode *head,*rear;
};
using stk=dstack*;
//初始化一个链栈（双链表实现，栈顶在链尾）
bool init(stk &s){
    s=new dstack;//初始化一个链栈，双链表实现，栈顶在链尾）
    dnode *p=new dnode;
    p->next=nullptr;
    p->pre=nullptr;
    s->head=p;
    s->rear=p;
    return true;
}
//判断栈是否为空
bool isempty(stk s){
    if(s->head==s->rear)
        return true;
    else 
        return false;
}
//入栈（在双链表链尾插入）
bool push(stk &s,int x){
    dnode *p=new dnode;
    p->data=x;
    p->next=nullptr;
    p->pre=s->rear;
    s->rear->next=p;
    s->rear=p;
    return true;
}
//出栈（删除双链表链尾元素）
bool pop(stk &s,int &x){
    if(isempty(s))
        return false;
    dnode *p=s->rear;
    x=p->data;
    s->rear=p->pre;
    s->rear->next=nullptr;
    delete p;
    return true;
}
C++

数组实现循环队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//数组实现循环队列

//定义队列
const int maxsize =100;
struct queue{
    int data[maxsize];
    int rear,head;
};

//初始化队列
void init(queue &q){
    q.rear=q.head=0;
}

//判断队空
bool isempty(queue q){
    if(q.head==q.rear)
		return true;
    else 
        return false;
    
}
//判断队满
bool isfull(queue q){
    if((q.rear+1)%maxsize==q.head)
        return true;
    else return false;
}
//入队
bool inqueue(queue &q,int x){
    if(isfull(q))return false;
    q.data[q.rear]=x;
    q.rear=(q.rear+1)%maxsize;
    return true;
}
//出队
bool outqueue(queue &q,int &x){
    if(isempty(q)) return false;
    x=q.data[q.head];
    q.head=(q.head+1)%maxsize;
    return true;
}

C++

单链表实现队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//单链表实现队列

//定义链表队列节点
struct qnode{
    int data;
    qnode *next;  
};

//定义队列
struct listqueue{
    qnode*head,*rear;
};
using lq=listqueue*;

//初始化队列
bool init(lq &q){
    q=new listqueue;
    qnode *p=new qnode;
    q->head=p;
    q->rear=p;
    p->next=nullptr;
    return true;
}
//判空
bool isempty(lq q){
    return q->head==q->rear;
}

//入队
bool inqueue(lq &q,int x){
    qnode *p=new qnode;
  	p->data=x;
    p->next=nullptr;
    q->rear->next=p;
    q->rear=p;
    return true;
}

//出队
bool outqueue(lq &q,int &x){
    if(isempty(q))return false;
    qnode *p=q->head->next;
    x=p->data;
    q->head->next=p->next;
    if(q->head->next==nullptr)
        q->rear=q->head;
    delete p;
    return true;
    
}
C++

树的一些代码模板

数组实现二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//数组实现二叉树(下标从1开始)

//定义树结点
struct treenode{
	int data;
    bool empty;
};
//初始化二叉树
void init(treenode t[],int length){
    for(int i = 0;i<length;i++)
        t[i].empty=true;
}
int main(){
    treenode t[100];
    init(t,100);
}
//判空树结点
bool isempty(treenode t[],int length,int x){
    if(x>=length || x<1) return true;
    return t[x].empty;
}
//找到结点的左孩子
int findlkid(treenode t[],int length,int x){
    int lkid = x*2;
    if(isempty(t,length,lkid))return -1;
    return lkid;
    
}
//找到结点的右孩子
int findrkid(treenode t[],int length,int x){
    int rkid = x*2+1;
    if(isempty(t,length,rkid))return -1;
    return rkid;
}

//找到结点的家长结点
int findparent(treenode t[],int length,int x){
    if(x==1)return -1;
    int parent=x/2;
    if(isempty(t,length,parent))return -1;
    return parent;
}
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//数组实现二叉树（下标从0开始）

//定义树结点
struct treenode{
	int data;
	bool empty;
};
//初始化
void init(treenode t[],int length){
	for(int i= 0;i<length;i++)
		t[i].empty=true;
}
int main(){
	treenode t[100];
	init(t,100);
    return 0;
}
//判空
bool isempty(treenode t[],int length,int x){
	if(x<0 || x>=length) return true;
	return t[x].empty;
}
//寻找家长节点
int findparent(treenode t[],int length,int x){
	if(x==0)return -1;
	int parent=(x-1)>>1;
	if(isempty(t,length,parent))return -1;
	return parent;
}
//寻找左孩子
int findlkid(treenode t[],int length,int x){
	int lkid = x*2+1;
	if(isempty(t,length,lkid))return -1;
	return lkid;
}

//寻找右孩子
int findrkid(treenode t[],int length,int x){
	int rkid=x*2+2;
	if(isempty(t,length,rkid))return -1;
	return rkid;
}
C++

二叉树的先中后序遍历

先序遍历
1
2
3
4
5
6
7
void visitnode(treenode &x);
void preorder(treenode t[],int length,int x){
        if(hisempty(t,lengt,x))return;   
            visitnode(t[x]);
            preorder(t,length,getlkid(t,length,x));
            preorder(t,length,getrkid(t,length,x));
}
C++
中序遍历
1
2
3
4
5
6
7
void visitnode(treenode &x);
void inorder(treenode t[],int length,int x){
    if(isempty(t,length,x)) return;
    inorder(t,length,getlkid(t,length,x));
    visitnode(t[x]);
    inorder(t,length,getrkid(t,length,x));
}
C++
后序遍历
1
2
3
4
5
6
7
void visitnode(treenode &x);
void postorder(treenode t[],int length,int x){
  if(isempty(t,length,x)) return;
  postorder(t,length,getlkid(t,length,x));
  postorder(t,length,getrkid(t,length,x));
  visitnode(t[x]);
}
C++

树的存储结构

双亲表示法
1
2
3
4
5
6
7
8
9
10
11
//定义树结点
const int maxsize=100;
struct ptnode{
    int data;
    int parent;
};
//定义树
struct ptree{
    ptnode nodes[maxsize];
    int n;
};
C++
孩子表示法
1
2
3
4
5
6
7
8
9
10
11
//定义孩子结点
const int maxsize=100;
struct kidnode{
    int index;
    kidnode *next;
};
//定义家长结点
struct parentnode{
	int data;
    kidnoe *firstkid;
}tree[maxsize];
C++
孩子兄弟表示法
1
2
3
4
5
6
//定义结点
struct node{
    int data;
    node*firstkid,*nextbrother;
};
using tree=node*;
C++

并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//定义并查集
const int N=100;
int size[N],p[N];
//初始化并查集
void init(int size[],int p[],int length){
    for(int i= 1;i<=length;i++)
    {
        size[i]=1;
        p[i]=i;
    }
}
//查
int find(int x){
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
//并
void merge(int a,int b){
    int r1=find(a);
    int r2=find(b);
    if(r1==r2)return;
    if(size[r1]>=size[r2]){
        p[r2]=r1;
        size[r1]+=size[r2];
    }
    else{
        p[r1]=r2;
        size[r2]+=size[r1];
    }
}
C++

图的一些代码模板

邻接矩阵实现图的顺序存储

1
2
3
4
5
6
7
//定义邻接矩阵
const int N =100;
struct graph{
    int n,e;
    char vex[N];
    int weight[N][N];
};
C++

邻接表实现图的链式存储

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const int N=100;
//定义弧结点
struct arcnode{
    int adjvex;//弧头结点的编号
    arcnode*nextarc;//指向下一条边的指针
    int info;//用来记录边的权值等信息
};
//定义顶点结点
struct vnode{
    char data;//结点所存储的字母
    arcnode *firstarc;//结点指向的第一条边
}
//定义邻接表
struct graph{
    vnode adjlist[N];//顶点结点数组
    int n,e;//边和顶点的数量
};
C++

dijkstra算法的文字过程描述

1
2
3
4
5
/*
从顶点x1出发，运行dijkstra算法的过程如下：
第一轮：顶点x1到x2的最短路径为1→2，距离为a
第n论：不存在顶点x1到顶点x2的路径，距离为∞
*/
C++

bfs算法的文字过程描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
    A
   / \
  B - C
  |   |
  D - E
       \
        F
//图的结构
/*
文字描述：用BFS算法求单源最短路径的过程
初始化：设置一个队列queue，用来存储要访问的结点，以A为起点，起点A入队，visit[A]=1,dist[A]=0

第一轮：队头是A，出队，将A的相邻结点B和C入队，更新dist[B]=1,dist[C]=1,visit[B]=1,visit[C]=1

第二轮：队头是B，出队，将B的相邻未访问节点D入队，dist[D]=2;visit[D]=1

第三轮：队头是C，出队，将C的相邻未访问结点E入队，dist[E]=2；visit[E]=1

第四轮：队头是D，出队，D无相邻未访问节点

第五轮：队头是E，出队，将E的相邻未访问节点F入队，dist[F]=3;visit[F]=1;
*/
C++

拓扑排序的文字过程描述

1
2
3
4
5
6
7
8
9
10
11
/*
拓扑排序：
1、从AOV网中选择任意一个入度为0的点，并将其加入拓扑序列
2、在AOV网中删除该点和以该点为起点的有向边
3、重复上述过程直到AOV网为空

逆拓扑排序：
1、从AOV网中选择任意一个出度为0的点，并将其加入拓扑序列
2、在AOV网中删除该点和以该点为起点的有向边
3、重复上述过程直到AOV网为空
*/
C++

关键长度的意义

1
2
/*AOE网的顶点代表时间，带权边代表活动，关键路径的长度代表的是
一个项目从开始到结束至少需要多长时间
C++

朴素版prim算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//
const int N=1000;
int n;
int g[N][N];
int dist[N];
bool st[N];
int prim(){
    int res=0;
    memset(dist,0x3f,sizeof(dist));
    for(int i = 0;i<n;i++){
        int t=-1;
        for(int j = 1;j<=n;j++)
            if(!st[j]&&(t==-1 || dist[t]>dist[j]))
                t=j;
        if(i && dist[t]==INF)return INF;
        if(i) res+=dist[t];
        st[t]=true;
        for(int j  = 1;j<=n;j++)
            dist[j]=min(dist[j],g[t][j]);
    }
    return res;
}
C++

排序的一些代码模板

快速排序

1
2
3
4
5
6
7
8
9
10
void quick_sort(int q[],int l,int r){
    if(l>=r)return ;
    int i  =  l-1,j=r+1,x=q[l+r>>1]
    while(i<j){
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j)swap(q[i],q[j]);
    }
    quick_sort(q,l,j),quick_sort(q,j+1,r);
}
C++

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void merge_sort(int q[],int l,int r){
	if(l>=r)return ;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
    int k = 0,i = l , j = mid+1;
    while(i<=mid && j <=r){
        if(q[i]<=q[j])tmp[k++]=q[i++];
        else tmp[k++]=q[j++];
    }
    while(i<=mid)tmp[k++]=q[i++];
    while(j<=r)tmp[k++]=q[j++];
    for(j = 0,i=l;i<=r;i++,j++)
        q[i]=tmp[j];
    
}
C++

查找的一些代码模板

二分查找

1

C++

错题本

2010 线性表 三次翻转

1
2
3
4
5
6
7
8
9
10
//自己的
void moveleft(int q[],int p,int n){
    int tmp[n];
    for(int i = 0;i<n;i++)
        tmp[(i+n-p)%n]=q[i];
    for(int i = 0 ;i<n;i++)
        q[i]=tmp[i];
    
    
}
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//标答
void reverse(int q[],int l,int r){
    if(l>=r)return;
    while(l<r){
        swap(q[l],q[r]);
        l++,r--;
    }
}
void moveleft(int q[],int n,int p){
    reverse(q,0,p-1);
    reverse(q,p,n-1);
    reverse(q,0,n-1);
}

C++

2011 线性表 二分搜索

1
2
3
4
5
6
7
8
9
10
11
12
//自己的
/*算法的基本设计思想：
中位数的位置是可以计算出的，也就是两个数列合并后处于L/2位置的数，利用两个指针ij分别指向数组A,B，然后找到第L/2大的数即中位数*/
int findmid(int a[],int b[],int l){
    int i = 0,j=0;
    while(i+j<l-1){
        if(a[i]>=b[j])j++;
        else i++;
    }
    return min(a[i],b[j]);
}
//14分
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//标答
int findMid(int a[], int b[], int n) {
    int l = 0, r = n;
    while (l < r) {
        int i = (l + r) / 2;
        int j = n - i;
        if (i < n && b[j - 1] > a[i]) l = i + 1;
        else if (i > 0 && a[i - 1] > b[j]) r = i - 1;
        else {
            int leftMax = 0;
            if (i == 0) leftMax = b[j - 1];
            else if (j == 0) leftMax = a[i - 1];
            else leftMax = std::max(a[i - 1], b[j - 1]);
            return leftMax;
        }
    }

    int i = l, j = n - l;
    if (i == 0) return b[j - 1];
    if (j == 0) return a[i - 1];
    return std::max(a[i - 1], b[j - 1]);
}
//15分
C++

2013 线性表 摩尔投票法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//自己的
//设计思想：如果一个数的出现次数大于n/2，那么他一定是这一组数顺序序列的中位数，然后找到比它小的第一个数和比他大的第一个数，两者的位置差就是该数出现的次数。
void quick_sort(int q[],int l,int r){
    if(l>=r)return ;
    int x=q[l+r>>1],i=l-1,j=r+1;
    while(i<j){
        do i++;while(q[i]<x);
        do j--;while(q[j]>x);
        if(i<j)swap(q[i],q[j]);
    }
    quick_sort(q,l,j),quick_sort(q,j+1,r);
}
int bsl(int l,int r,int x,int q[]){
    while(l<r){
        int mid=l+r+1>>1;
        if(q[mid]<x)l=mid;
        else r=mid-1;
    }
    return l;
}
int bsh(int l,int r,int x,int q[]){
    while(l<r){
        int mid = l+r>>1;
        if(q[mid]>x)r=mid;
        else l  = mid+1;
    }
    return l;
}
int findmain(int a[],int n){
    quick_sort(a,0,n-1);
    int result = a[n-1>>1];
    int left=bsl(0,n-1,result,a);
    int right=bsh(0,n-1,result,a);
    if(right-left-1>(n>>1))return result;
    else return -1;
}

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//摩尔投票法，时间复杂度O(n)，空间复杂度O(1)
int find_main(int a[], int n) {
    int candidate = -1, count = 0;

    // 第一轮：找出可能的主元素
    for (int i = 0; i < n; i++) {
        if (count == 0) {
            candidate = a[i]; // 换人
            count = 1;
        } else if (a[i] == candidate) {
            count++; // 同类+1
        } else {
            count--; // 异类-1
        }
    }

    // 第二轮：验证是否真的是主元素（必须超过一半）
    count = 0;
    for (int i = 0; i < n; i++) {
        if (a[i] == candidate) count++;
    }

    return (count > n / 2) ? candidate : -1;
}
C++

🎭 这个算法其实是在模拟“投票大战”！

想象你现在有一群人，每人代表一个数。你的目标是找出 有没有某个数在这群人里占多数（超过一半）。

🥊 摩尔投票的逻辑是：

  • 你一开始不知道谁是主角，所以从第一个人开始猜；
  • 如果后来遇到和当前猜测一样的人（站你这边），你就信心 +1；
  • 如果遇到和你猜的不一样的人（反对你），你就信心 -1；
  • 如果信心掉到 0，就说明你现在这个候选人支持和反对打平了，需要换人重新开始；
  • 最后剩下来的“赢家”有可能是主角，但得再数一遍确认一下它是不是真的超过一半。

🎯 那为什么 count-- 是必要的？

因为每遇到一个“不同”的数，就是“主元素”的一个反对票。

如果主元素真的超过一半，那其他所有数都不够把它抵消掉，它一定能撑到最后！

比如数组：

1
2
3
4
5
csharp


复制编辑
[5, 5, 3, 5, 7, 5, 5, 1]
ACCESSLOG
  • 主元素是 5，它有 5 票；
  • 剩下的 3、7、1 只有 3 票；
  • 即使这 3 票全都拿来反对 5，5 还是赢了！

所以你在每遇到一个“异类”时，就等于主角被反对了一次，要 count--。

✅ 总结一句话：

count-- 是为了让反对的声音抵消掉主元素的票数，看它能不能最终剩下来。

2018 线性表 原地哈希法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//自己的
//设计思路：将数组变为有序数组，从最小的正整数1开始判断数组中是否出现，然后递增找到最小的未出现正整数
void quick_sort(int a[],int l,int r){
    if(l>=r)return;
    int x=a[l+r>>1],i=l-1,j=r+1;
    while(i<j){
        do i++ ;while(a[i]<x);
        do j--;while(a[j]>x);
        if(i<j)swap(a[i],a[j]);
    }
    quick_sort(a,l,j),quick_sort(a,j+1,r);
}
int findmin(int a[],int n){
    int mini = 1;
    quick_sort(a,0,n-1);
    for(int i = 0 ; i<n;i++){
        if(a[i]==mini) mini++;
    }
    return mini;
}
//时间复杂度O(nlogn)空间复杂度O(logn)

C++
1
2
3
4
5
6
7
8
9
10
11
//课本上的答案 时间复杂度O(n),空间复杂度O(n)
int findmin(int a[],int n){
    int tmp[n];
    memset(tmp,0,sizeof(tmp));
    for(int i = 0;i<n;i++){
        if(a[i]>0&&a[i]<=n)tmp[a[i]-1]=1;

    }
    for(int i = 0;i<n;i++)
        if(!tmp[i])return i+1;
}
C++
1
2
3
4
5
6
7
8
//更好的答案（原地哈希法）时间复杂度O(n)，空间复杂度O(1)
int findmin(int a[],int n){
    for(int i = 0 ;i<n;i++)
        while(a[i]>0 && a[i]<=n &&a[a[i]-1]!=a[i])
          swap(a[a[i]-1],a[i]);
    for(int i = 0;i<n;i++)
        if(a[i]!=i+1)return i+1;
}
C++

2020 线性表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//答案
const int maxint = 0x3f3f3f3f
bool ismin(int a,int b,int c){
    return a<=b&&a<=c;
}
int distance(int a[],int n1,int b[],int n2,int c[],int n3){
    int i = 0 ,j=0,k = 0,dmin = maxint;
     	while(i<n1  && j<n2&& k <n3 &&d>0){
            int d = abs(a[i]-b[j])+abs(a[i]-c[k])+abs(b[j]-c[k]);
            if(d<dmin) dmin=d;
            if(ismin(a[i],b[j],c[k]))i++;
            else if(b[j],a[i],c[k]) j++;
            else k++;
        }
    return  dmin;
}

C++

2009 单链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//自己的
#include <iostream>
using namespace std;
struct lnode{
    int data;
    lnode *next;
};
using linklist = lnode*;
int getlength(lnode* head){
    int length=0;
    lnode *p=head->next;
    while(p){
        length++;
        p=p->next;
    }
    return length;
}
int findnum(lnode *head,int k){
        int length=getlength(head);
        int n=length-k+1;
        lnode *p=head->next;
        for(int i = 1;i<n;i++){
                p=p->next;
                if(!p)return 0;
        }
        cout<<p->data<<endl;
        return 1;
}
    //描述算法的基本设计思想：第一遍顺序查找遍历一遍链表，获取链表长度，然后计算倒数k个位置对应的是正数第n-k+1个位置，第二遍顺序查找到第n-k+1个节点，如果存在，输出对应的值并返回1，如果不存在则返回0
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//答案的
/*思路
1)算法的基本设计思想：
问题的关键是设计一个尽可能高效的算法，通过链表的一次遍历，找到倒数第k个结点的位置。定义两个指针变量p和q,初始时均指向头结点的下一个结点(链表的第一个结点),p指针沿链表移动；当p指针移动到第k个结点时，q指针开始与p指针同步移动；当p指针移动到最后一个结点时，q指针所指示结点为倒数第k个结点。以上过程对链表仅进行一遍扫描。
2)算法的详细实现步骤如下：
1、count=0,p和q指向链表表头结点的下一个结点。
2、若p为空，转5。
3、若count等于k,则q指向下一个结点；否则，count=count+1。
4、p指向下一个结点，转2。
5、若count等于k,则查找成功，输出该结点的data域的值，返回1;否则，说明k值超过了线性表的长度，查找失败，返回0。算法结束。
*/
#include <iostream>
using namespace std;
struct lnode
{
    int data;
    lnode *next;
};
int findnum(lnode *list,int k){
    lnode *p=list->next;
    lnode *q=list->next;
    int count = k;
    while(count--){
        if(p==nullptr)return 0;
        p=p->next;

    }
    while(p){
        p=p->next;
        q=q->next;
    }
    if(q==nullptr) return 0;
       
    cout<<q->data<<endl;
    return 1;

}
C++

2012 单链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//自己的
#include <iostream>
using namespace std;
struct lnode
{
    char data;
    lnode *next;
    bool ispass=0;
};
using linklist=lnode *;
linklist findpoint(lnode *str1,lnode *str2){
    while(str1){
        str1->ispass=1;
        str1=str1->next;    
    }
    while(str2){
        if(!(str2->ispass)){
            str2->ispass=1;
            str2=str2->next;
        }
        else break;
    }
    lnode *p=str2;
    return p;
}
//思路：先遍历一遍str1，标记已经遍历过的节点，然后再遍历一遍str2，当str2遍历到已经标记过的节点，说明其是二者共同后缀的起始位置。时间复杂度为O(n)

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//答案
#include <iostream>
using namespace std;
struct node
{
    char data;
    node *next;
};
int listlen(node *head){
    int len=0;
    while(head->next!=nullptr){
        len++;
        head=head->next;
    }
    return len;
}
//找出共同后缀的起始地址
node * findlist(node *str1,node *str2){
    int m,n;
    node *p,*q;
    m=listlen(str1);
    n=listlen(str2);
    for(p=str1;m>n;m--)p=p->next;
    for(q=str2;m<n;n--)q=q->next;
    while (p->next!=nullptr&&p->next!=q->next)
    {
        p=p->next;
        q=q->next;
    }
    return p->next;
}
C++

顺序遍历两个链表到尾结点时，并不能保证两个链表同时到达尾结点。这是因为两个链表的长度不同。假设一个链表比另一个链表长k个结点，我们先在长链表上遍历k个结点，之后同步遍历两个链表，这样就能够保证它们同时到达最后一个结点。因为两个链表从第一个公共结点到链表的尾结点都是重合的，所以它们肯定同时到达第一个公共结点。
1)算法的基本设计思想：
①分别求出str1和str2所指的两个链表的长度m和n。
②将两个链表以表尾对齐：令指针p、q分别指向str1和str2的头结点，若m≥n,则指针p先走，使p指向链表中的第m-n+1个结点；若m<n,则使q指向链表中的第n-m+1个结点，即使指针p和q所指的结点到表尾的长度相等。
③反复将指针p和q同步向后移动，并判断它们是否指向同一结点。当p、q指向同一结点，则该点即所求的共同后缀的起始位置。

2015 单链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//自己的
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
struct node
{
    int data;
    node*link;  
};
void delnode(node *p){//删除该节点的下一个节点
        node *q=p->link;
        p->link=q->link;
        free(q);
}
void nosame(node *head,int m,int n){
    bool ispass[n+1];
    memset(ispass,0,sizeof(ispass));
    node *p=head->link;
    while (p)//同时保存两个点，一个是当前节点的上一个节点即head所指向的，一个是当前节点即p
    {
        if(!(ispass[abs(p->data)])){
            ispass[abs(p->data)]=1;
            p=p->link;
            head=head->link;
        }
        else{
            delnode(head);
            p=head->link;
        }
    }
    
}
/*思路：用一个bool数组记录某个数曾经出现过，
如果遍历到某个点的时候发现他的绝对值出现过，则删除该点。时间复杂度为O(m)*/
C++
1
2
//答案
同样
C++

2019 单链表 快慢指针找链表中点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//自己的
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;


/*
思路：根据题目可知，会被插入的节点有n-1/2（下取整）个，即从n-(n-1/2)后面都是要插入前面序列的节点
从该点开始对后面的采用头插法二次插入，形成一个后部逆序，然后从头开始隔次插入，即可得到题目要求的结果
*/
struct node
{
    int data;
    node *next;
};
int getlength(node *head){
    node *p=head->next;
    int length=0;
    while(p){
        length++;
        p=p->next;
    }
    return length;
}

void insertlist(node *head){
    int n=getlength(head);
    int k = n-(n-1>>1);
    node *h=head->next;
    for(int i = 1;i<k;i++){
            h=h->next;//跳出循环后p指向的是第k个节点，也就是不需要倒插的最后一个节点,相当于倒置链表的头结点
    }
    int m = n-1>>1;
    node *p=h->next;
    node *tmp=p->next;
    p->next=nullptr;
    p=tmp;
    //从第一个点开始头插，用一个指针保存剩下的链表的开头
    for(int i = 1;i<=m;i++){
        node *tmp=p->next;//剩下待插入的链表的起点
        p->next=h->next;
        h->next=p;
        p=tmp;     
    }//形成倒插序列
    node *p=h->next;
        node *q=head->next;
        int count= n;
        node *rear=head;
    while (count)
    {//n个数重组
       //顺序链表取数
       node *tmp=q->next;
       rear->next=q;
       rear=q;
       q=tmp;
       count--;
       //逆序链表取数
        node *tmp=p->next;
        rear->next=p;
        rear=p;
        p=tmp;
        count--;
    }
    rear->next=nullptr;
}
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//答案
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;


/*
思路：根据题目可知，会被插入的节点有n-1/2（下取整）个，即从n-(n-1/2)后面都是要插入前面序列的节点
从该点开始对后面的采用头插法二次插入，形成一个后部逆序，然后从头开始隔次插入，即可得到题目要求的结果
*/
struct node
{
    int data;
    node *next;
};
void changelist(node *h){
    node *p,*q,*r,*s;
    p=q=h;
    while (q->next!=nullptr)//寻找中间节点
    {
        p=p->next;
        q=q->next;
        if(q->next!=nullptr) q=q->next;
    }
    q=p->next;//p所指节点为中间节点，q为后半段链表的首节点
    p->next=nullptr;//p为中间节点，将中间节点指向的节点变为nullptr
    while (q!=nullptr)
    {
        //将链表后半段逆置,p(中间节点)充当了头结点的地位，q成为了待插入链表的起点
        r=q->next;//r用来存储下一个要插入的节点
        q->next=p->next;//头插法，q指向原头结点指向的节点
        p->next=q;//q成为头结点指向的节点
        q=r;//q成为下一个要插入的节点
    }
    s=h->next;//s指向前半段的第一个数据节点，即插入点
    q=p->next;//q指向后半段的第一个数据节点
    p->next=nullptr;//p要成为链表的
    while (q!=nullptr)//将链表后半段的节点插入到指定位置
    {
        r=q->next;//r指向后半段的下一个节点
        q->next=s->next;//将q所直接点插入到s所指结点之后
        s->next=q;
        s=q->next;//s指向前半段的下一个插入点
        q=r;//q变为后半段要插入的点
    }
    

    
}
C++

你问：“为什么快指针 q 走两步，慢指针 p 走一步，最后 q 到达链尾时 p 正好在链表中间？”

这个其实是快慢指针（龟兔赛跑）找链表中点的经典原理，我给你详细解释一下：

原理说明

  • 设链表长度为 n。
  • 慢指针 p 每次走一步，快指针 q每次走两步。
  • 当快指针 q 到达链表末尾（或越过末尾）时，慢指针 p 所指节点就是链表的中点。

为什么成立？

  • 由于 q速度是 p的两倍，假设 p走了 k 步，那么 q走了 步。

  • 当 q 到链尾时，链表总长度是 n，因此：

  • 即慢指针 p 走了链表长度一半的步数，停在中点。

直观示例

链表长度 q走的步数 p 走的步数 p 位置
5 4~5 2~3 第3个节点（中间）
6 6 3 第4个节点（中间）

代码示例

1
2
3
4
5
6
7
8
9
node* findMiddle(node* head) {
    node* p = head;
    node* q = head;
    while (q != nullptr && q->next != nullptr) {
        p = p->next;
        q = q->next->next;
    }
    return p; // p 指向中点
}
CPP

总结

  • 快指针两步，慢指针一步。
  • 快指针到末尾时，慢指针刚好走一半，指向中点。
  • 这是链表中点查找的最常用技巧。

形象文字图

1
2
3
4
5
6
7
less复制编辑节点： 1 → 2 → 3 → 4 → 5 → 6 → 7 → nullptr

p:        ↑     ↑     ↑     ↑
         1     2     3     4

q:        ↑           ↑           ↑
         1           3           5           7
APACHE
  • 每次循环，p向右走一个节点，q向右走两个节点。
  • 当q到达链尾或超出链尾时，p所在的位置就是中点。

2022 二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//自己的
#include <iostream>
using namespace std;
/*
思路：遍历数组的每个点，判断各点是否符合二叉搜索树的情况，时间复杂度为O(n)
*/
const int max_size =10000;
struct sqbitree{
    int sqbitnode[max_size];
    int Elenum;
};
bool isbst(sqbitree a){
        int n = a.Elenum;
        for(int i = 0;i<n;i++){
            int x=a.sqbitnode[i];
            int lk=a.sqbitnode[i*2+1];
            int rk=a.sqbitnode[i*2+2];
            if(x==-1)continue;
            if(x>=lk &&x<=rk)continue;
            else return false;
        }
        return true;
}
C++
1
//答案
C++

2023 邻接矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//我的
#include <iostream>
#include <cstring>
using namespace std;
const int MAXV=1000;
struct MGraph
{
    int numVertices,numEdges;
    char VerticesList[MAXV];
    int Edge[MAXV][MAXV];
};
/*
思路：遍历邻接矩阵，当Edge[a][b]有值的时候说明存在一条a->b的边，也就是a的出度+1，b的入度+1，
遍历完整个邻接矩阵后即可得到所有点的入度和出度，时间复杂度为O(V²)
*/

int printVertices(MGraph G){
    int n = G.numVertices;//点的数量
    int m = G.numEdges;//边的数量
    int innum[n];//记录每个顶点的入度
    int outnum[n];//记录每个顶点的出度
    memset(innum,0,sizeof(innum));
    memset(outnum,0,sizeof(outnum));
    for(int i = 0;i<n;i++){
        for(int j = 0 ;j<n;j++)
          {
            if(m<=0) break;//剪枝
            if(G.Edge[i][j]) {
                innum[j]++;//j为终点，入度+1
                outnum[i]++;//i为起点，出度+1
                m--;//遍历完一条边
            } 
          }
    }
    int count=0;
    for(int i= 0;i<n;i++){
        if(outnum[i]>innum[i]){
            cout<<char(i+97);
            count++;
        }
    }
    return count;
}
C++

2021 邻接矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//自己的
#include <iostream>
#include <cstring>
#define INF 0x3f3f3f3f
using namespace std;
const int MAXV=1000;
struct MGraph
{
    int numVertices,numEdges;
    char VerticesList[MAXV];
    int Edge[MAXV][MAXV];
};
/*
思路：不大于2的偶数，即0或者2，我们可以遍历整个数组，计算每个顶点的度，然后再遍历一遍存储度的数组，
当度为奇数的顶点个数超过2就return 0，如果最后结果是2或者0就break；同时由于是无向图，数组为对称矩阵，
可以采用压缩存储的思路减少遍历的数组元素
时间复杂度O(v²)空间复杂度O(V);
*/
int IsExistEL(MGraph G){//假设不存在
        int n = G.numVertices,m=G.numEdges;//用n存储顶点数，m存储边数
        int dexnum[n];
        memset(dexnum,0,sizeof dexnum);
        for(int i = 0;i<n;i++){
            for(int j = 0 ;j<i+1;j++){
                if(m == 0) break;
                if(G.Edge[i][j] && G.Edge[i][j]!=INF) {
                    dexnum[i]++;
                    dexnum[j]++;
                    m--;
                }
            }
        }
        int count = 0;
        for(int i = 0;i<n;i++){
                if(count >2) return 0;
                if(dexnum[i]%2) count++;
        }
        if(count ==0 || count == 2)return 1;
        else return 0;
        
}

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//答案
#include <iostream>
#include <cstring>
#define INF 0x3f3f3f3f
using namespace std;
const int MAXV=1000;
struct MGraph
{
    int numVertices,numEdges;
    char VerticesList[MAXV];
    int Edge[MAXV][MAXV];
};
int IsExistEL(MGraph G){//假设不存在
        int degree;
        int count = 0;
        for(int i = 0;i<G.numVertices;i++){
            degree =0;
            for(int j = 0;j<G.numVertices;j++)
                degree+=G.Edge[i][j];
            if(degree%2) count ++;
        }
        if(count==0 ||count==2)return 1;
        else return 0;
        
}

C++

2024 拓扑序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//自己的
时间复杂度O(n²)空间复杂度O(1)
#include <iostream>
#include <cstring>
using namespace std;
const int MAXV=1000;
struct MGraph
{
    int numVertices,numEdges;//图的顶点数和有向边数
    char VerticesList  [MAXV];//顶点表
    int Edge[MAXV][MAXV];//邻接矩阵，无权图
};
/*
思路：拓扑序列唯一，说明每次可以加入拓扑序列的入度为0的点是唯一的，然后同时说明拓扑序列存在，
因此只需要判断每次入度为0的点是否唯一，且当入度为0的点为0的时候，是否还有顶点没有加入拓扑序列，如果全部加入，
则存在唯一的拓扑序列
*/
int uniquely(MGraph G){
    int n =G.numVertices;
    int d[n];//存储每个顶点的入度
    memset(d,0,sizeof d);
    for(int j = 0;j<n;j++)//遍历每个顶点
        for(int i = 0;i<n;i++)//每个顶点和其他顶点是否有入边
            d[j]+=G.Edge[i][j]; 
        //找到入度为0的点
    int hh=-1;
    for(int k = 0;k<n;k++){//n个点循环n次
        int dot ;
        for(int i = 0;i<n;i++){//找到入度为0的点加入拓扑序列
            if(!d[i])
            {
                ++hh;//加入拓扑序列
                dot = i;
                d[i]=-1;//从图中删除点i
            }
           } 
            if(hh!=k) return 0;//按理来说一次加入一个入度为0的点，从而拓扑序列唯一，如果加入两个，说明不唯一
        for(int j = 0;j<n;j++)
            if(G.Edge[dot][j]) d[j]--;//从图中删除该点为起点的边
    }
    if(hh==(n-1)) return 1;//每个点都加入了拓扑序列
    else return 0;//有点没有加入拓扑序列


}

C++

2016 排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//自己的
#include <iostream>
using namespace std;
/*
思路：将集合排序，然后将较小的一半当作A1，较大的一般当作A2，即符合题目的要求,时间复杂度O(nlogn)，空间复杂度O(n)
*/
void quick_sort(int a[],int l,int r){
    if(l>=r)return ;
    int i = l-1,j=r+1;
    int x = a[l+r>>1];
    while (i<j)
    {
        do i++;while(a[i]<x);
        do j--;while(a[j]>x);
        if(i<j)swap(a[i],a[j]);
    }
    quick_sort(a,l,j),quick_sort(a,j+1,r);
    
}
void grouping(int n,int a[]){
        quick_sort(a,0,n-1);
        int n1=n>>1;//小半边
        int n2=n-n1;//大半边
        int a1[n1];//小
        int a2[n2];//大
        for(int i = 0;i<n1;i++) a1[i]=a[i];//小
        for(int i = n1,j=0;i<n;i++,j++)a2[j]=a[i];
}
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//答案
#include <iostream>
using namespace std;
/*
思路：将集合排序，然后将较小的一半当作A1，较大的一般当作A2，即符合题目的要求,时间复杂度O(nlogn)，空间复杂度O(n)
*/
int setPartition(int a[],int n){
    int pivot,low = 0,low1=0,high=n-1,high1=n-1,flag=1,k=n>>1,i;
    //枢纽值，第一组的起点和终点，第二组的起点和终点，判断是否退出循环，中间值的位置
    int s1=0,s2=0;//大小两个组的和
    while (flag)
    {
        pivot=a[low];//第一个值为枢纽
        while(low<high){//双指针分组
            while(low<high && a[high]>=pivot) --high;
            if(low!=high) a[low]=a[high];
            while(low<high && a[low]<=pivot) ++low;
            if(low!=high) a[high]=a[low];
        }
        a[low]=pivot;//把枢轴值放到正确位置
        if(low == k-1)//如果数周是第n/2小的位置，划分成功
            flag =0;
        else{
            if(low <k-1)//说明该枢纽值属于较小的一边,继续划分右半部分
               {
                 low1=++low;//右半部分从枢轴右端开始（参考二分）
                high=high1;//右半部分的右端是n
               }
            else{//说明枢轴属于较大的一边，继续划分左半部分
                low = low1;
                high1=--high;
            }
            
        }
    }
    for(int i = 0;i<k;i++)s1+=a[i];
    for(int i = k;i<n;i++)s2+=a[i];
    return s2-s1;    

}
C++
#408日常
数据结构算法笔试
http://example.com/2025/04/02/数据结构算法笔试/
作者
Kugeln
发布于
2025年4月2日
许可协议