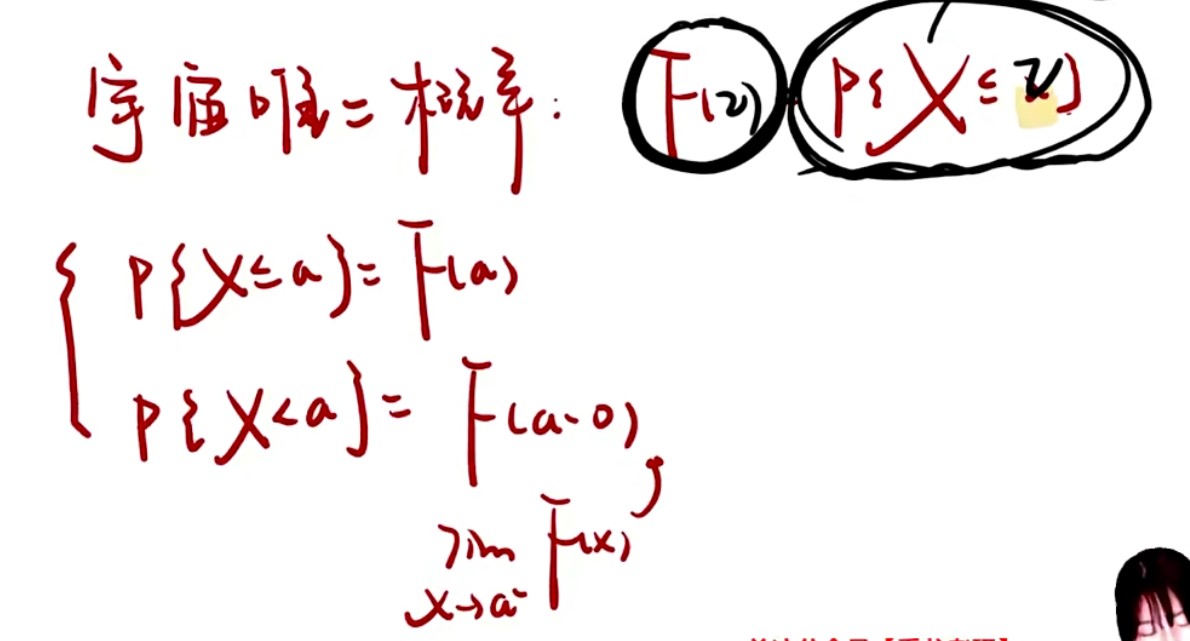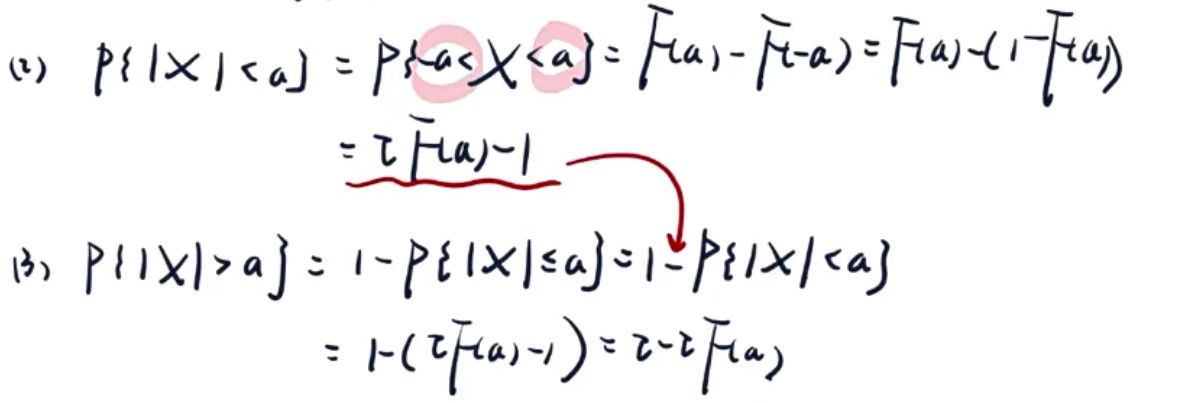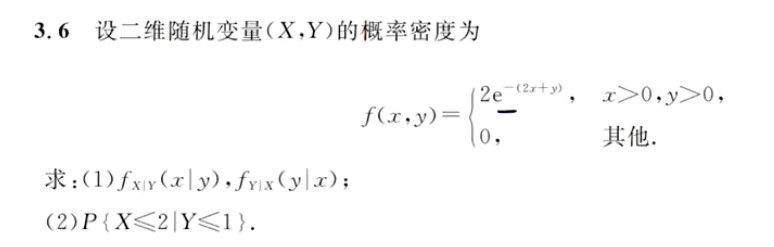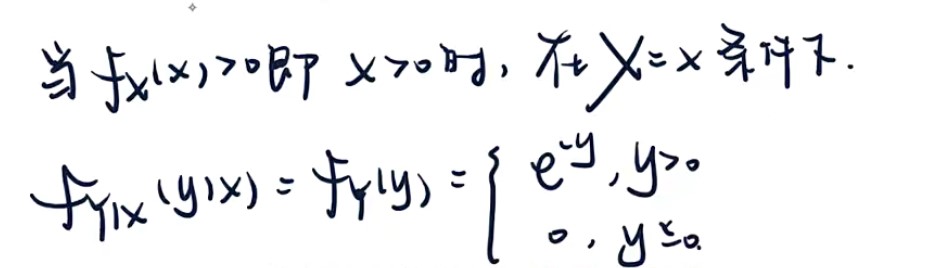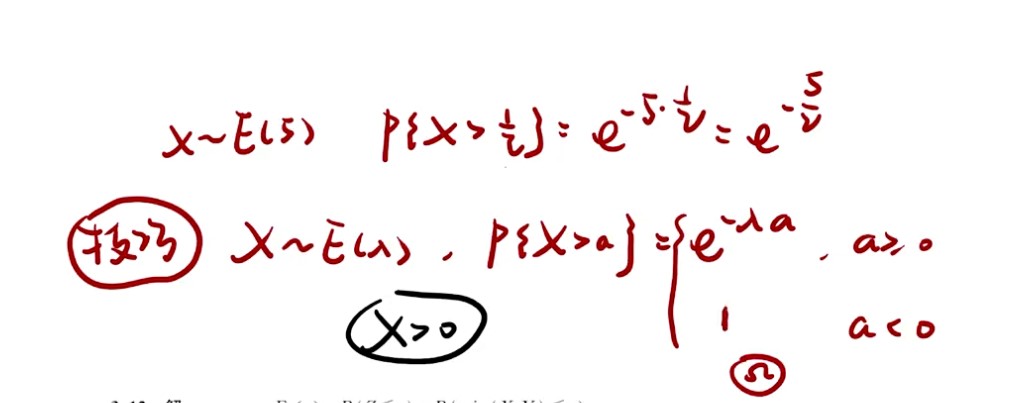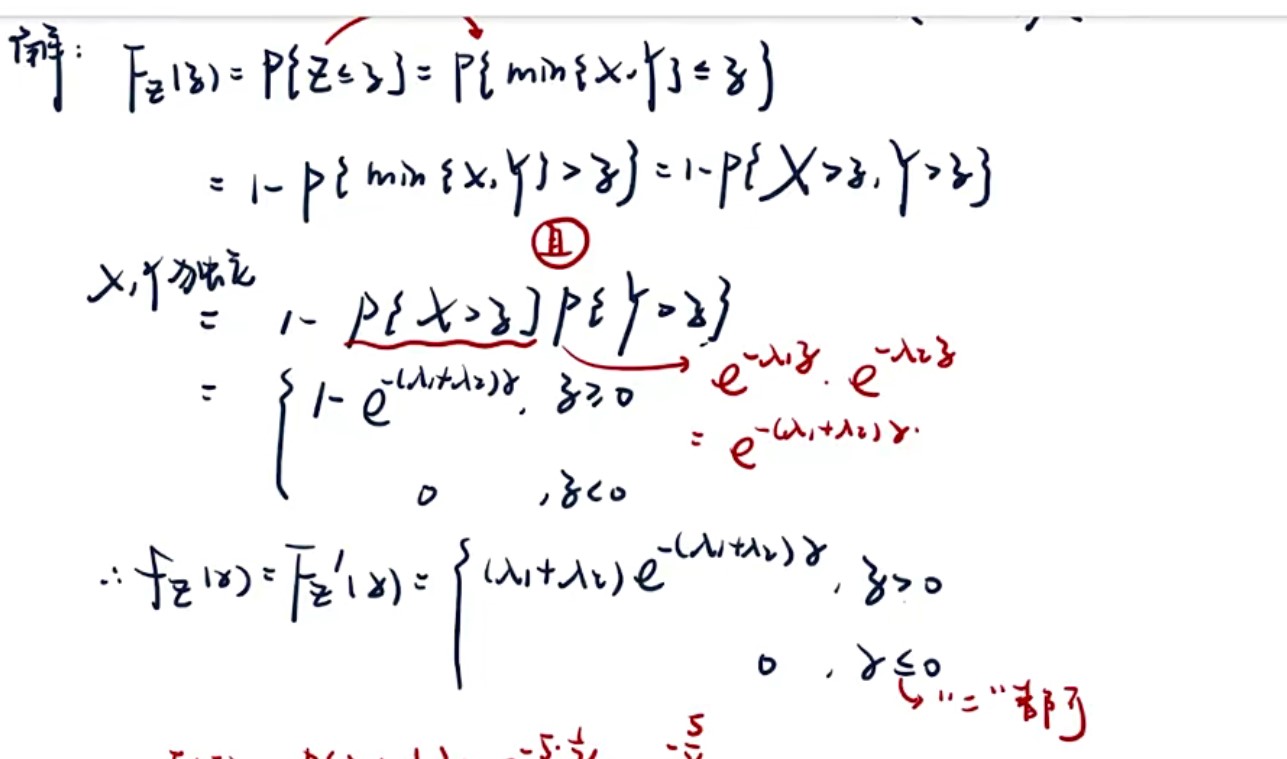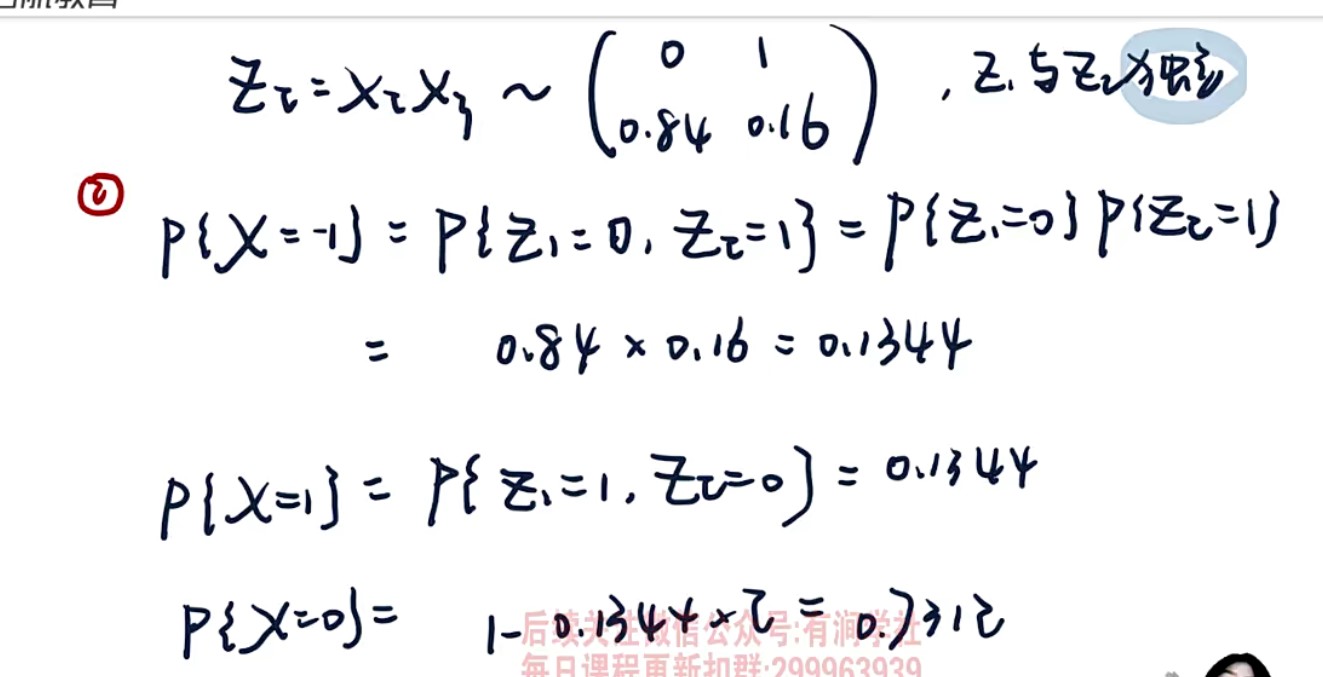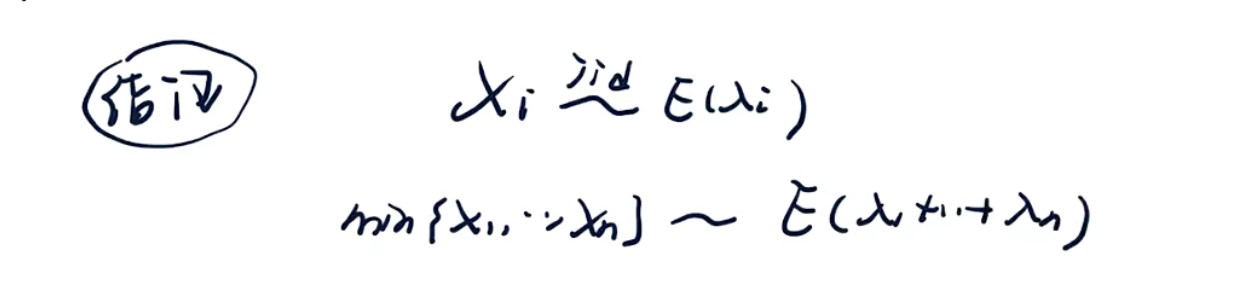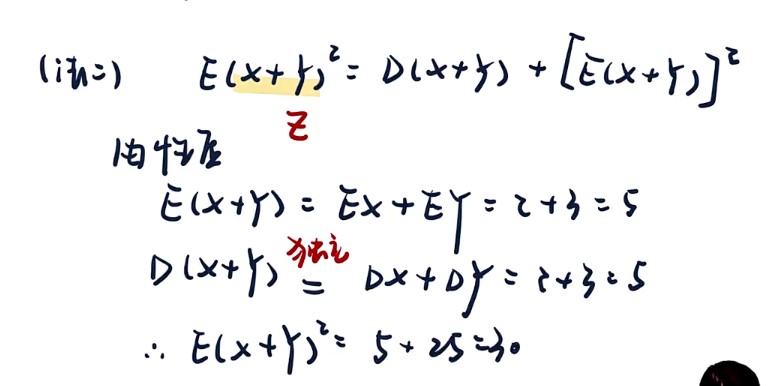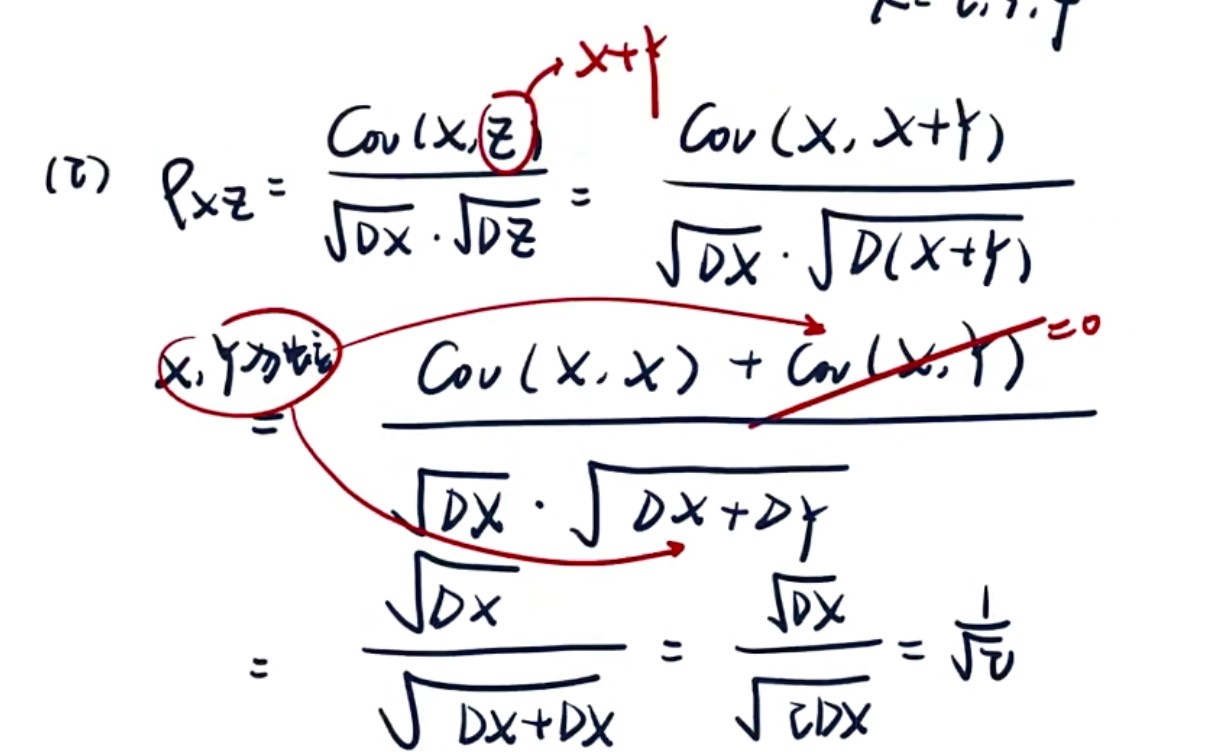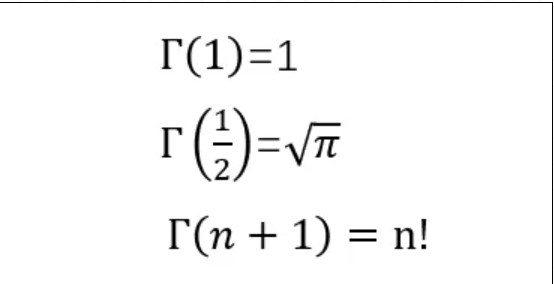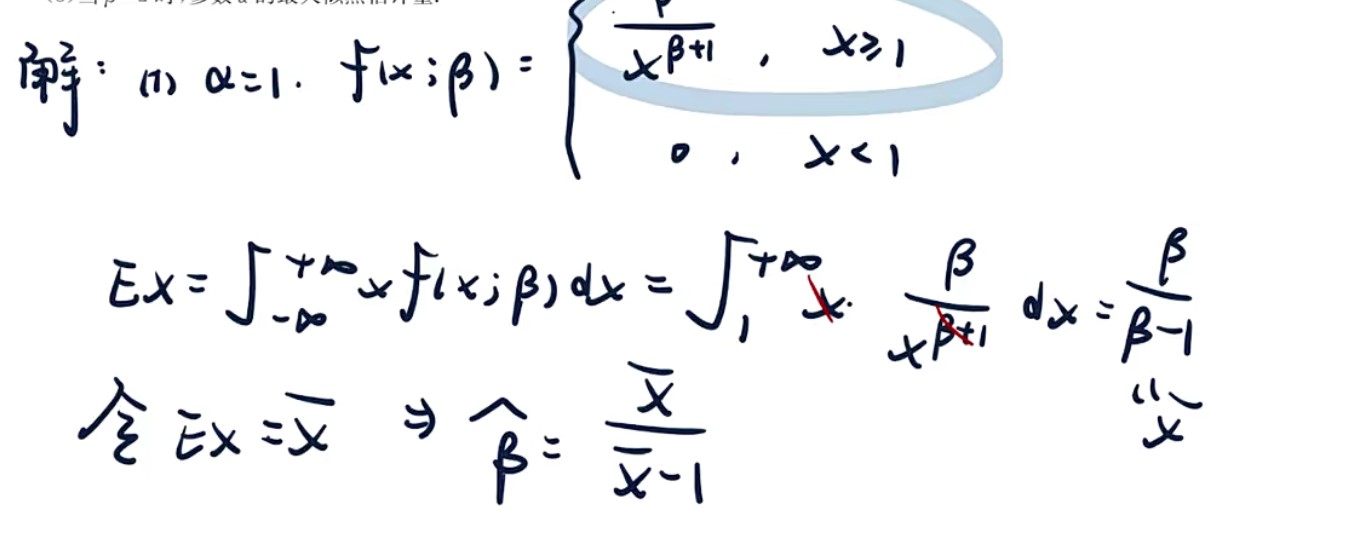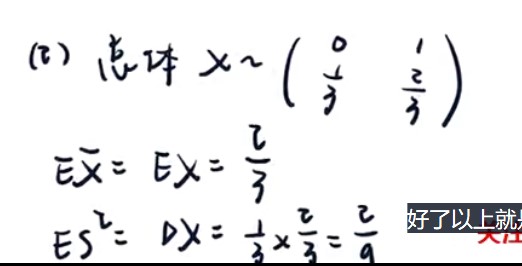概率论错题

随机事件与概率

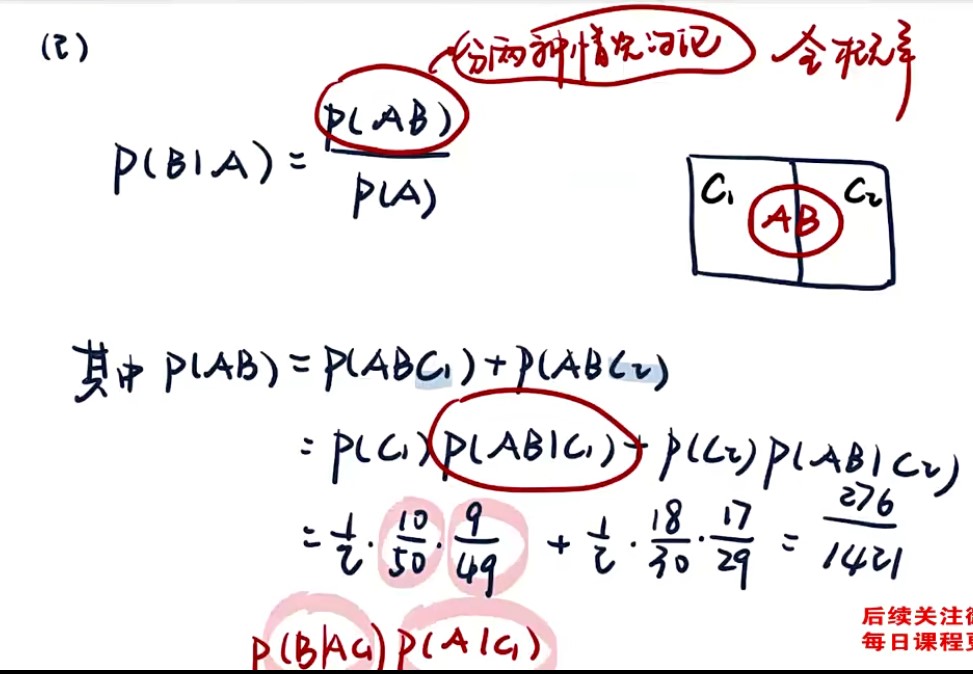
1

2

3

4

5

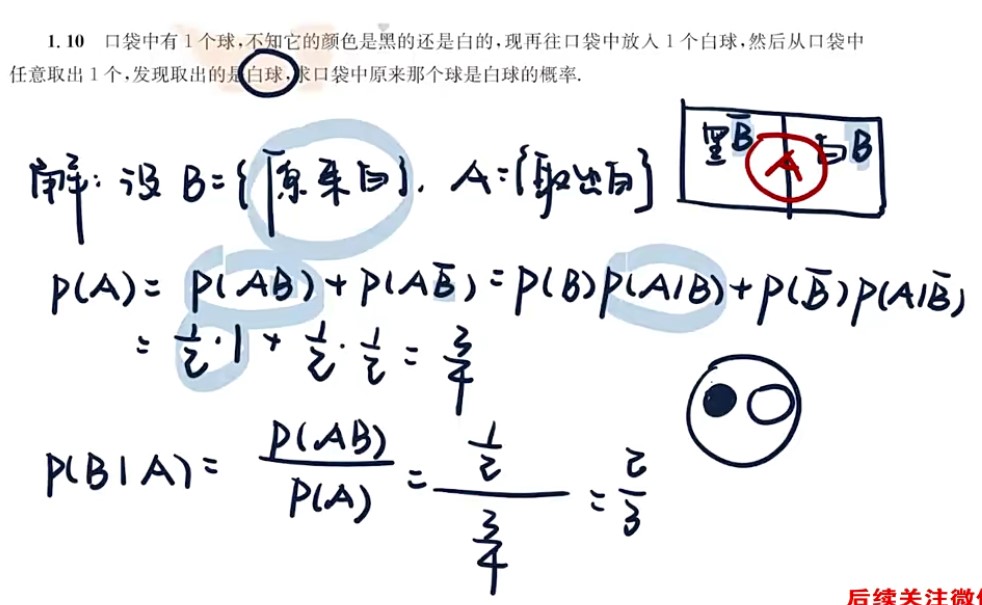
6

7

8

9

一维随机变量及其分布

题型总结

• 判断是否是分布函数/概率密度

  • 利用分布函数和概率密度的性质

• 已知分布函数F(x)求概率

  • 宇宙唯二概率+抠

  

• 离散型X分布律的两要素和充要条件

  • X分布律的取值x和对应概率p
    • p≥0
    • ∑p=1

• 已知概率密度f(x)，求分布函数F(x)/求概率

  • 概率密度永远写开区间
  • 一般分布函数F(x)等号永远跟着大于走，永远保证右连续性

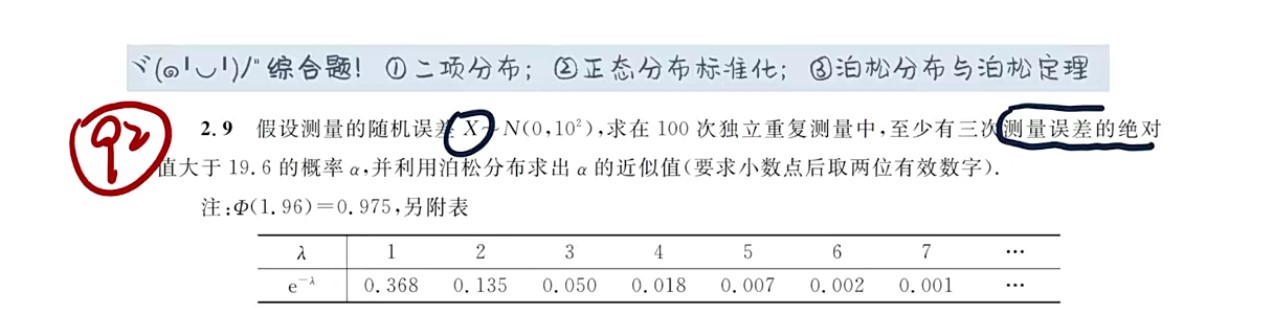
• 二项分布题型

  • 优先写出X~B(n,p)，其中n为独立重复实验次数，p为事件A发生的概率

  

  

• 句式杂糅的句子成分分析技巧：

  • 有xx次xxx发生的概率为
    • 次后圈A
    • 设次数为Y

• 离散型所有情况概率相加，连续型求积分

• 已知X的概率密度f(x)，求Y=g(x)的分布——分布函数法

  • 先看X的类型
    • X是离散型，Y是分布律：取值，概率
    • 连续性
  • 把Y换成X，从关于Y的概率变为关于X的概率
    • 大写字母就是随机变量，整个概率就是关于大写字母的概率，要用大写字母的分布去写，题目里概率的事件里面谁是大写就是关于谁的概率，用谁的分布
    • 小写字母是p里面的常数，当作常数
  • Y是分段函数，X是概率密度
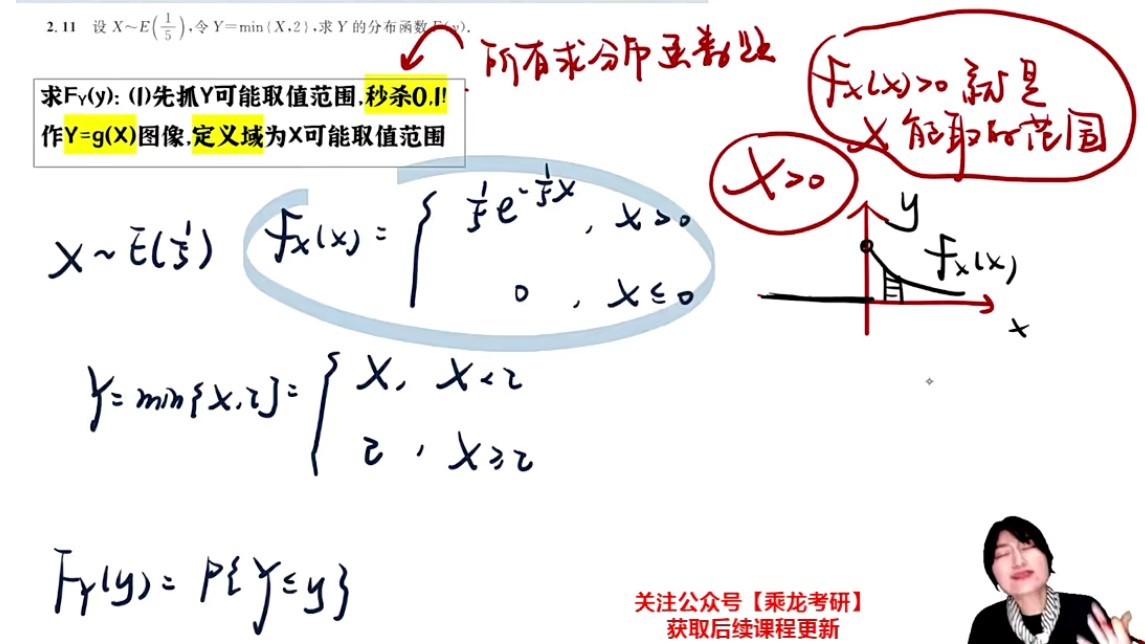
    • 求FY(y)：
      • 先抓Y可能取值范围，秒杀0，1，作Y=g(X)的图像，定义域为X可能取值范围
      • 在Y的取值范围内，作直线Y=y，取下方部分将{Y≤y}转化为X的范围（直线与Y=g(X)有几种交法，就分几段讨论）
  • Y是离散型
    *

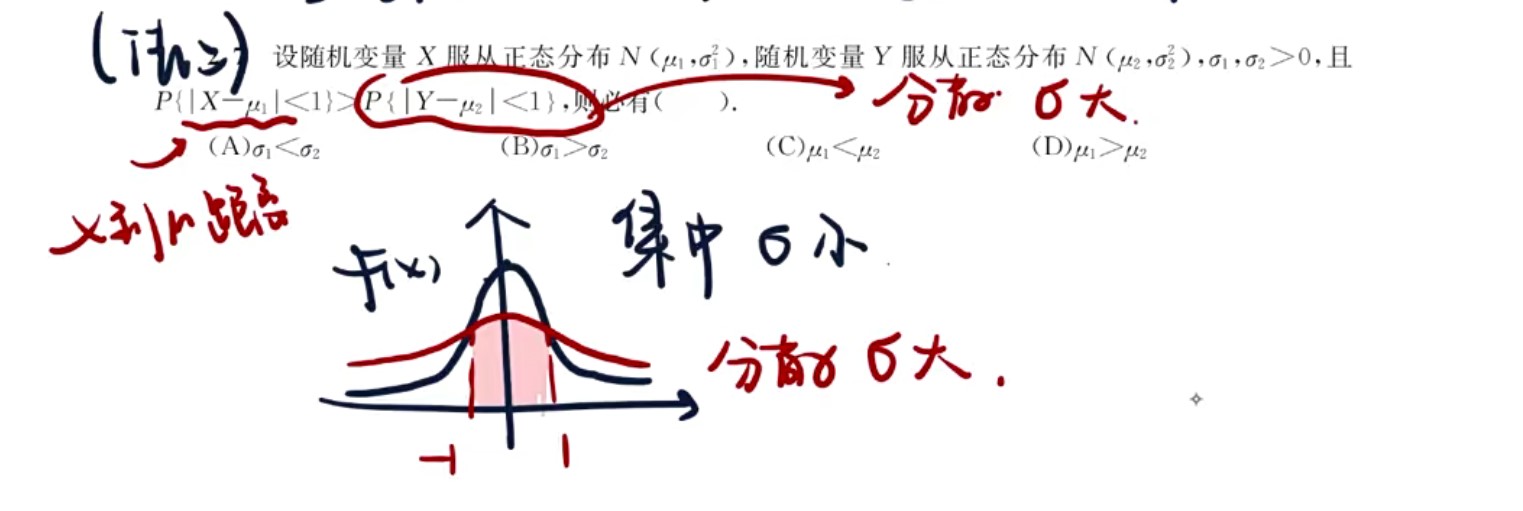
• 若X的可能取值范围在a到b之间，当x<a时，F(x)=0,当x>b时，F(x)=1

  • 对离散型，连续型，混合型通用

• 离散型阶梯型的各点概率密度等于1从后往前减

  • 离散型X已知分布律：所有情况都找出来，概率相加

1

2

3

4

5

• 思路：
  • 根据X的范围反求出Y的范围
  • 作出Y=y的直线，左下方是X的范围，把y当常数


6

7

8

9

10

11

多维随机变量及其分布

1

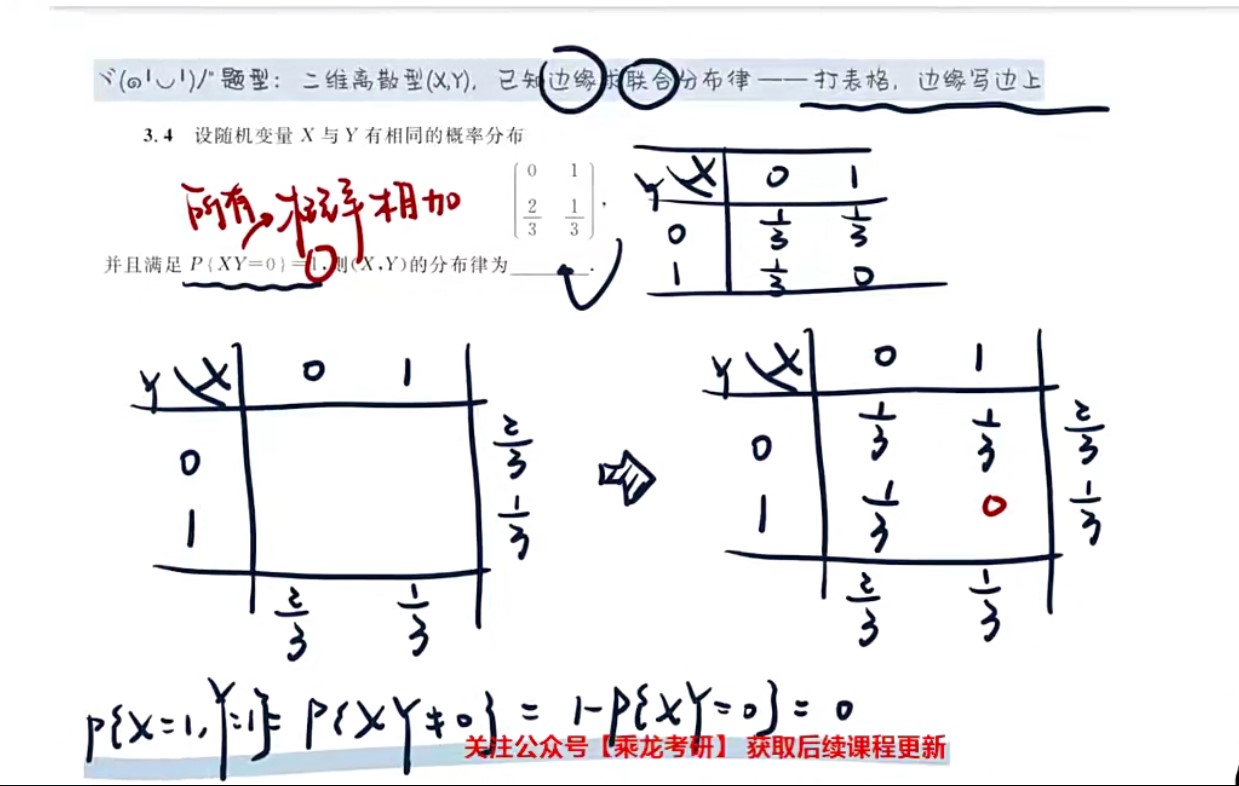
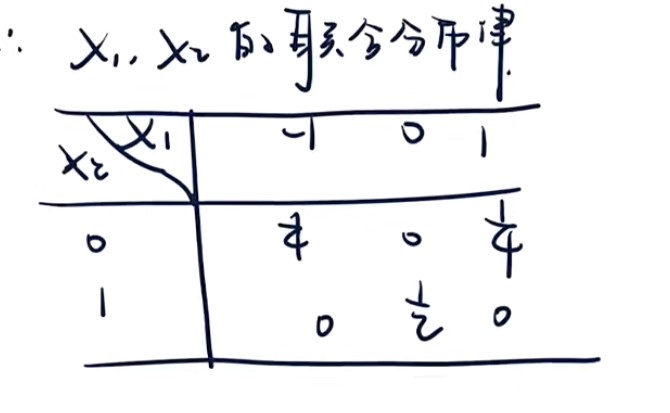
• 已知边缘求联合分布律——打表格，边缘写边上

2

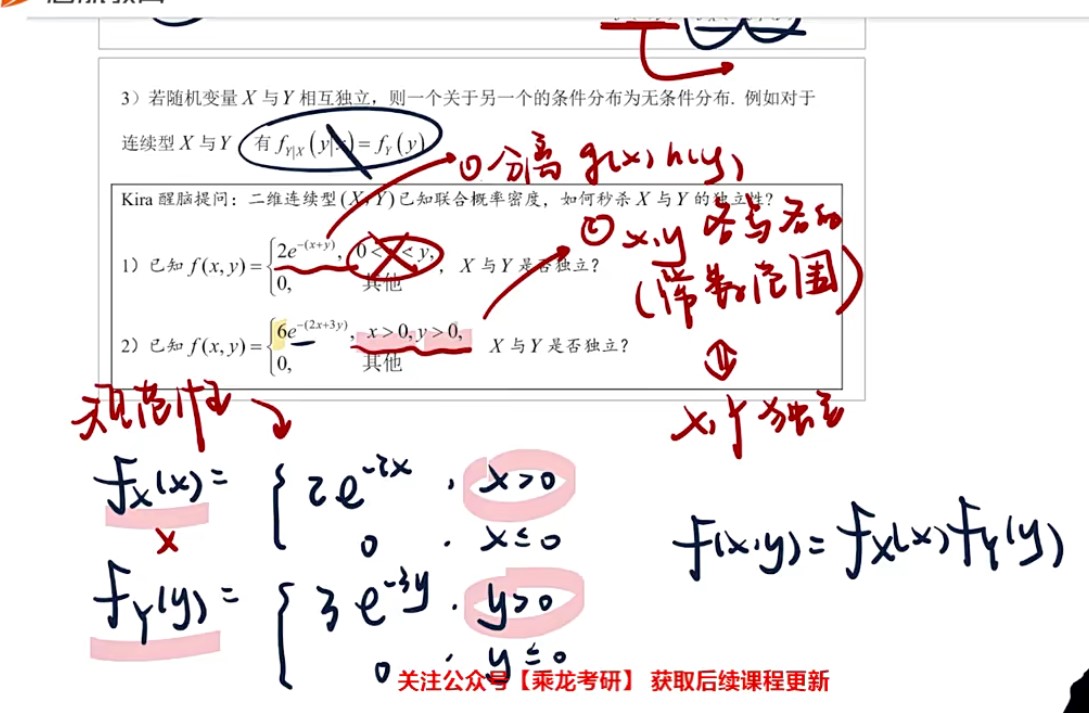
• 条件概率密度仅限于二维连续型
• 只要一个二元函数，能够拆成两个一元函数相乘，则X与Y相互独立
  • 一看前面的函数部分，可不可以分离成g(x)h(y)
  • 二看xy是不是各写各的范围，或者是不是都是常数范围

3

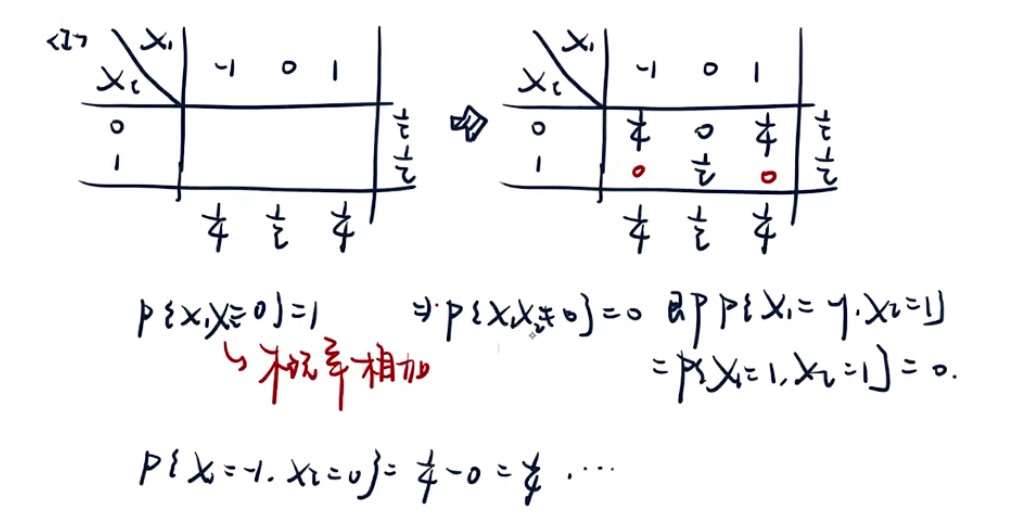
• 离散型二维随机变量独立性判断技巧
  • 只要pij出现0，XY一定不独立
  • X,Y独立⇿行（列）对应成比例（秩为1）

4

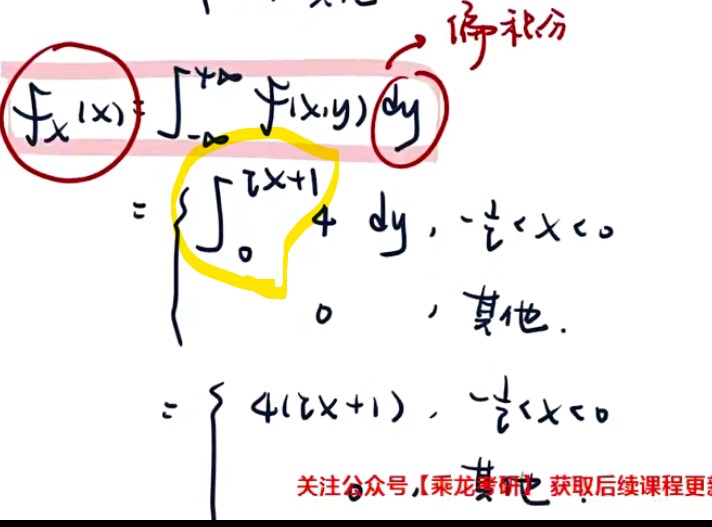
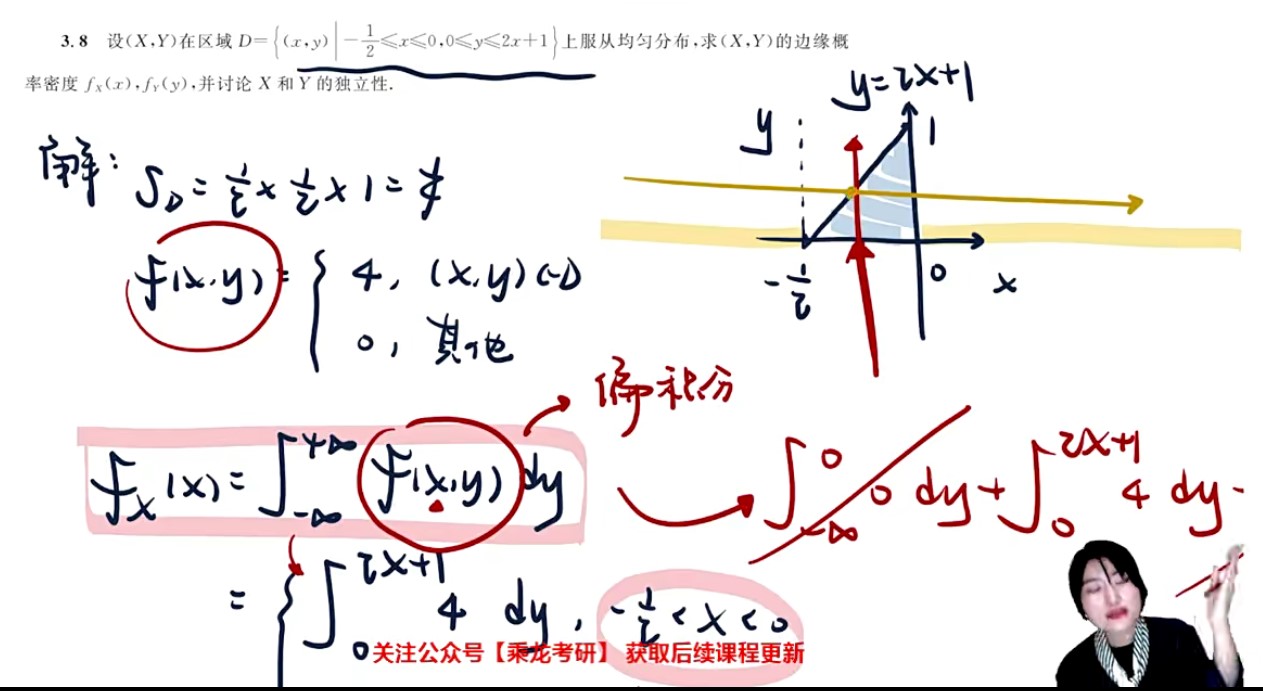
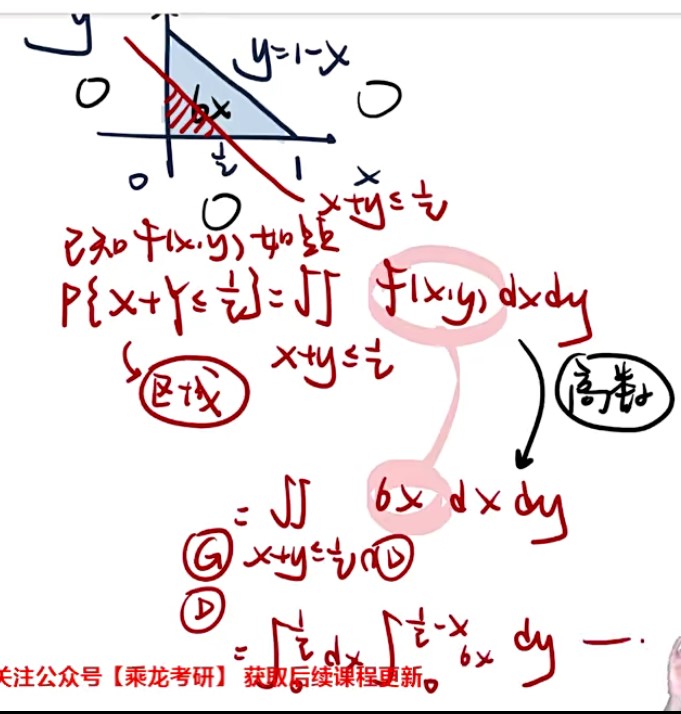
• 求谁不积谁（求X是对X型区域积分，求Y是对Y型区域积分）

• 不积先定限

• dy画竖线，dx画横线（限内画条线，先交取下限，后交取上限）

5

6

7

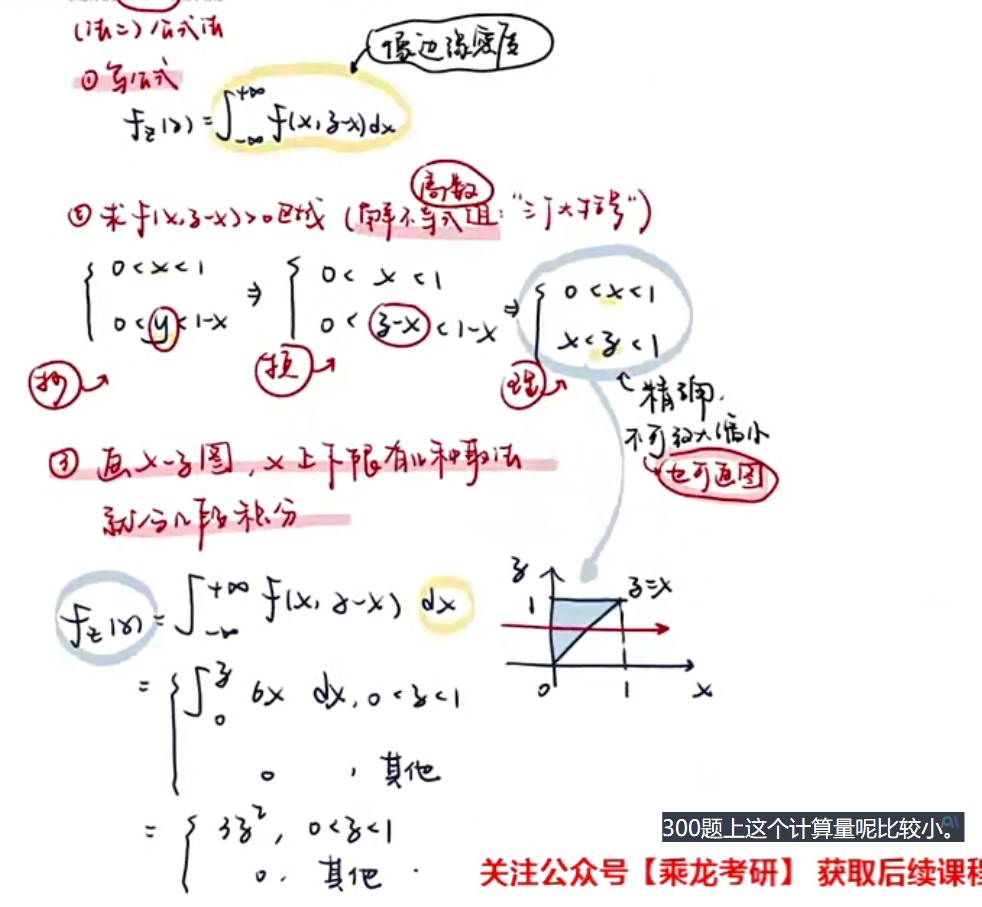
• 题型：最大最小值分布

• 指数分布技巧：

• 如果n个随机变量互相独立且分别服从指数分布，那么他们的最小值分布依然是服从指数分布，参数就是他们的参数相加

8

• 题型：求Z=g（X,Y）的分布——X，Y一个离散型一个连续型（分布函数法+对离全集分解）

9

• 二维(X,Y)求概率，X，Y一个离散型一个连续性（对离全集分解）

10

11

12


13

14

• 题型：已知Y在X满足一定条件下的条件分布，求Y的分布函数F(y)

随机变量的数字特征

1

• 题型：已知f(x)求EX+期望的性质

2

• 题型：数学期望应用题

3

• 题型：利用性质，求相关系数

4

• 题型：判断是否相关

5

6

7

8

9

大数定律与中心极限定理

1

2

• 简单随机样本：独立同分布

3

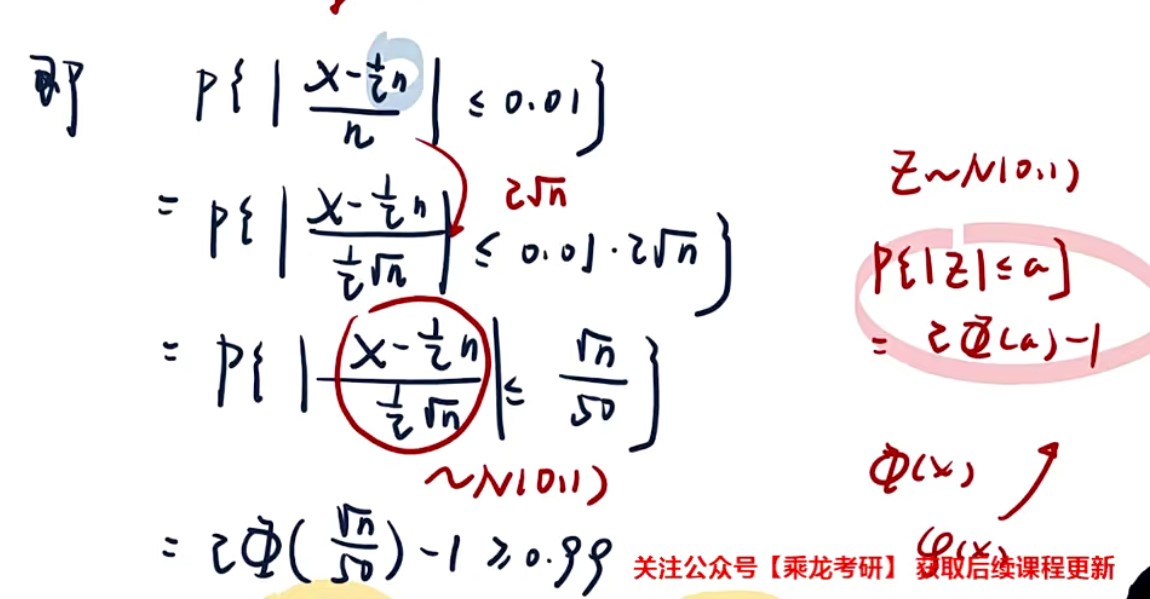
• 求谁的平均，验谁的条件

4

5

数理统计

抽样分布：统计量（X拔和S²，样本构成的不含未知参数的函数）的分布

1

2

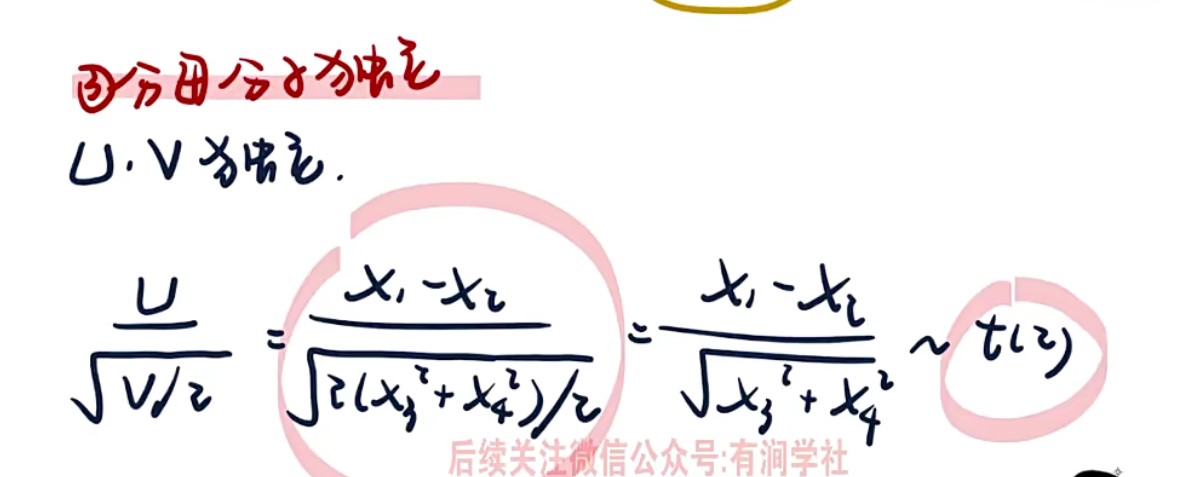
• 化标准（修复）的方法

U/根号（V/自由度）

3

4

5

• 最大似然估计是函数的最值问题，要让似然函数达到最大，去求这个θ

6

7

8

9

10

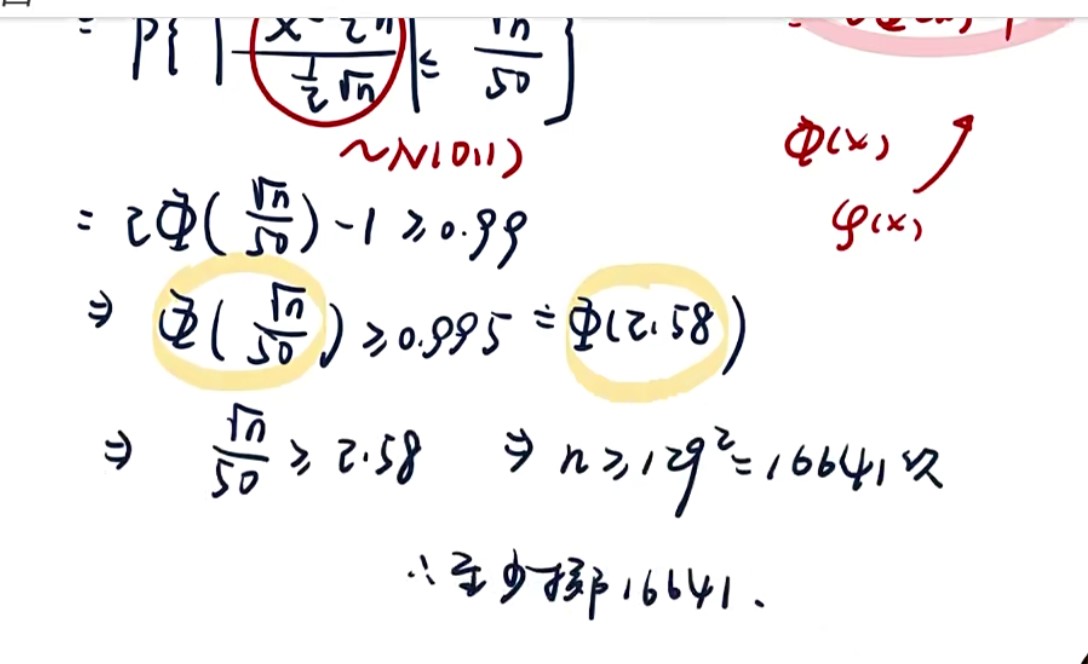
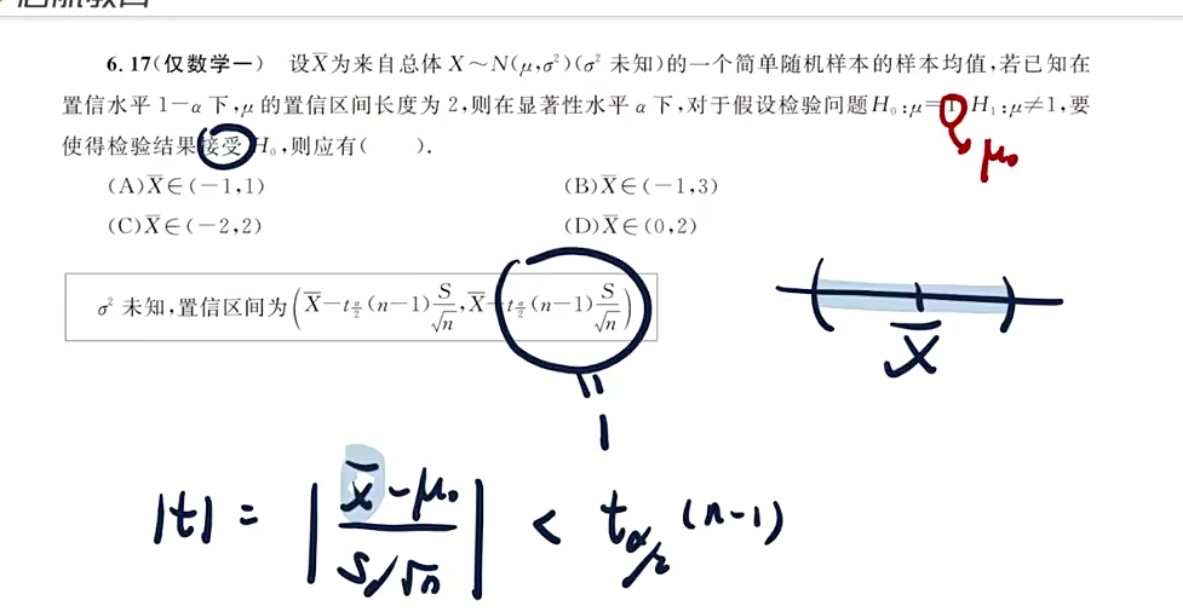
• 题型：正态总体抽样分布——抓整体形势（系数差一点就错）

11

12

13

14

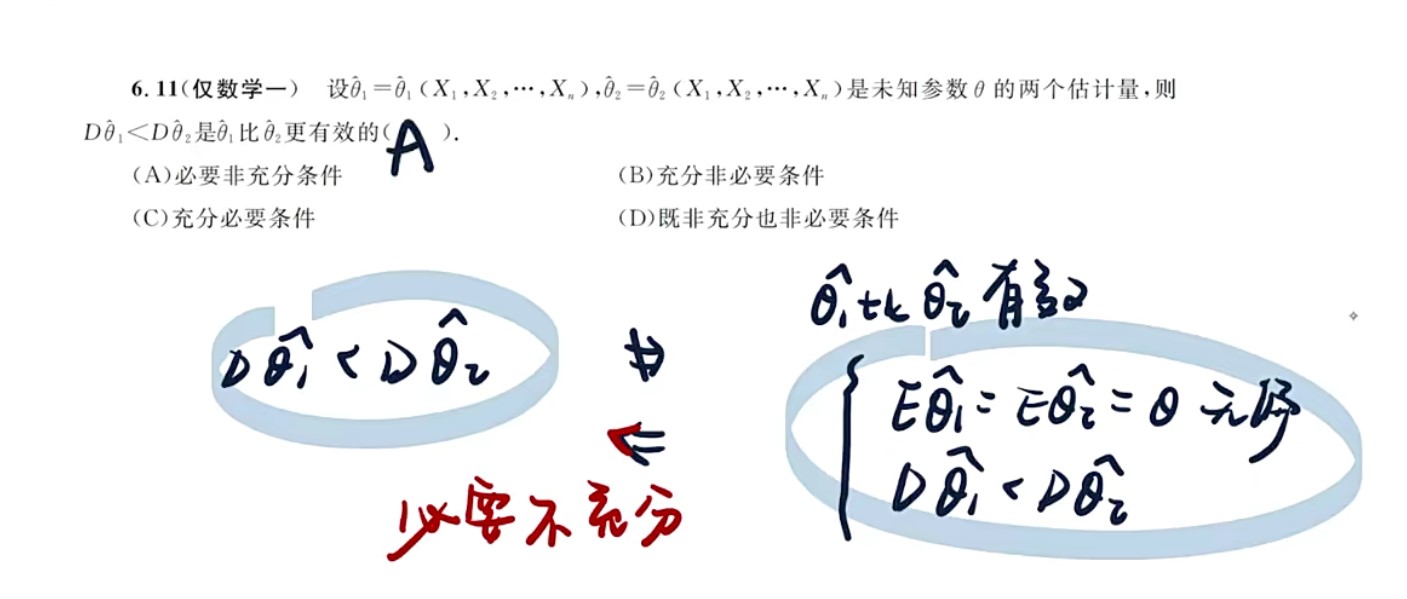
• 左必右充

15

16

17

18

• 单调增加没有驻点就取样本值的最大最小值（一般表现为x的范围与θ有关）

19