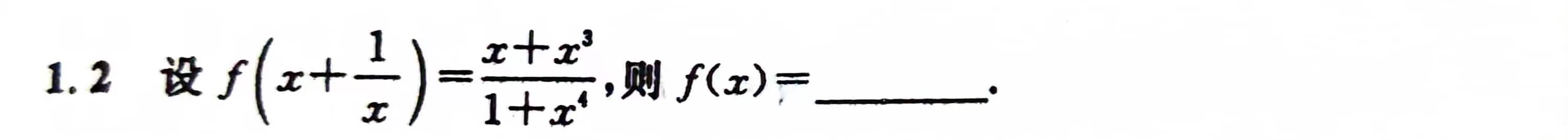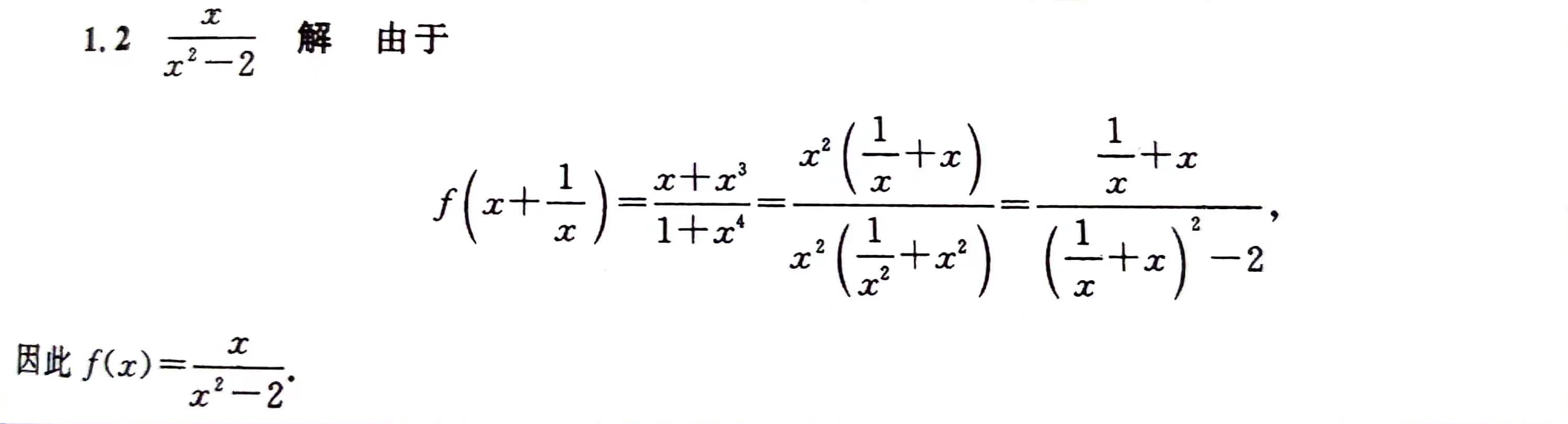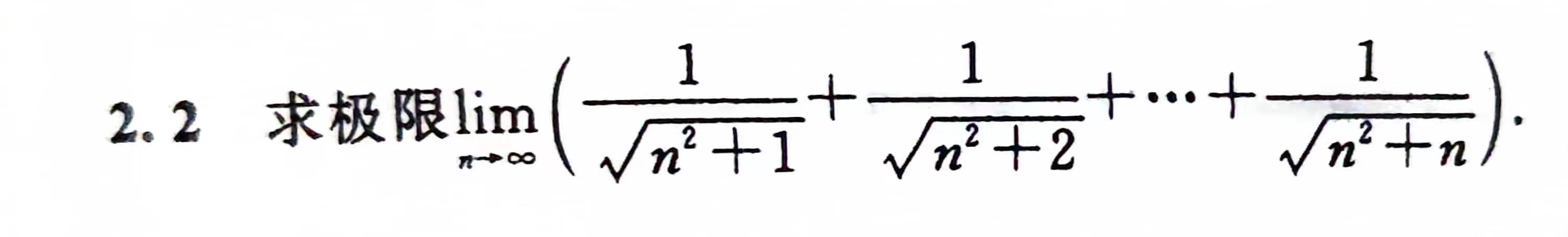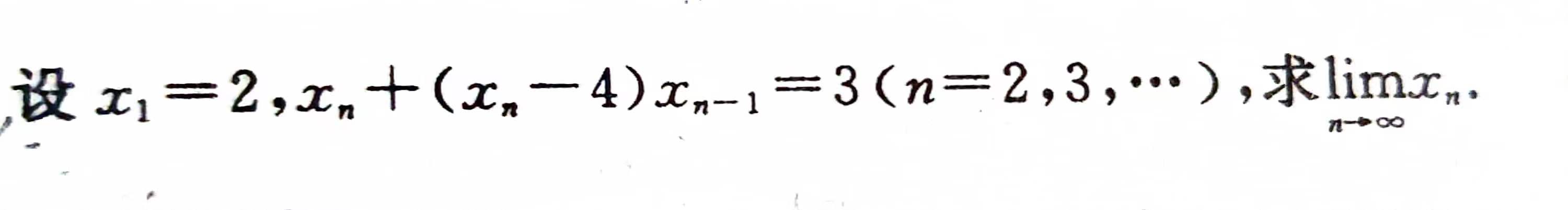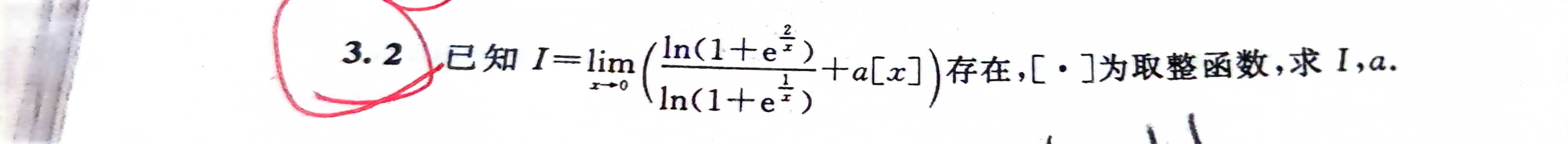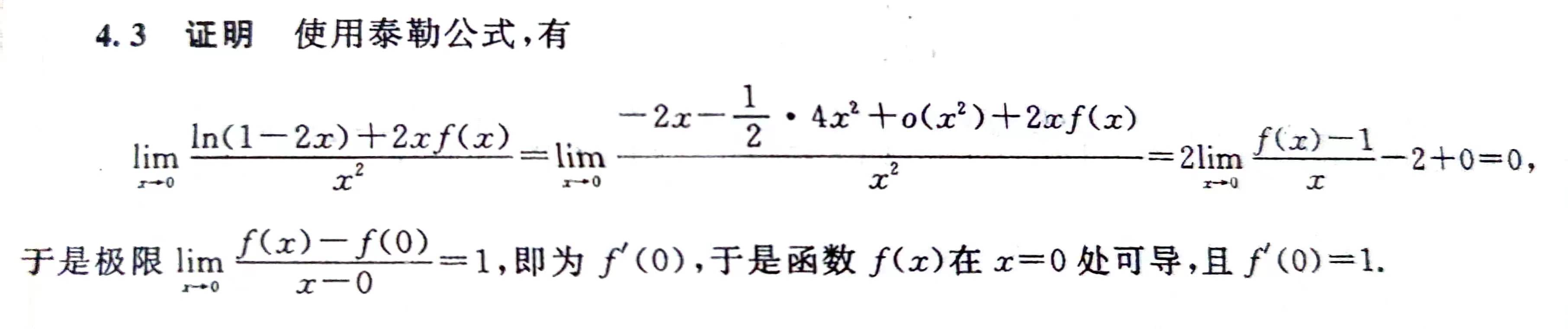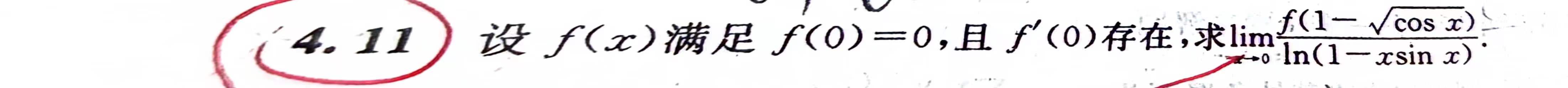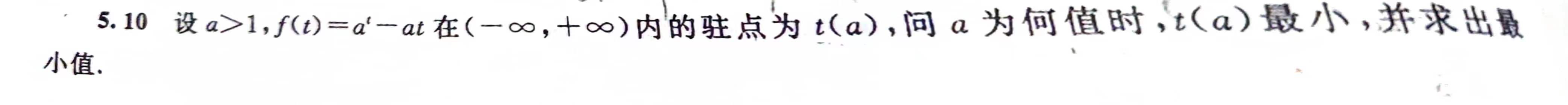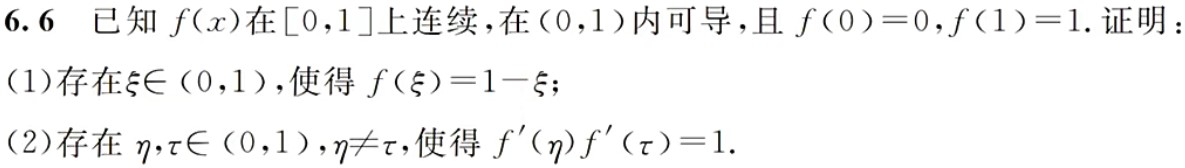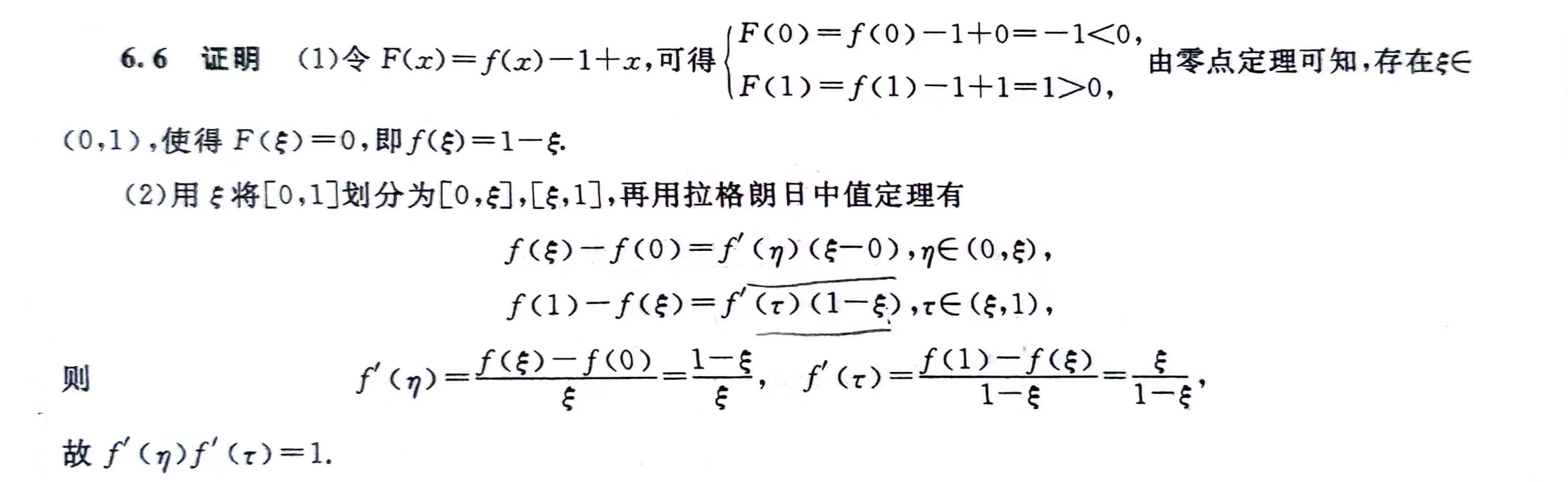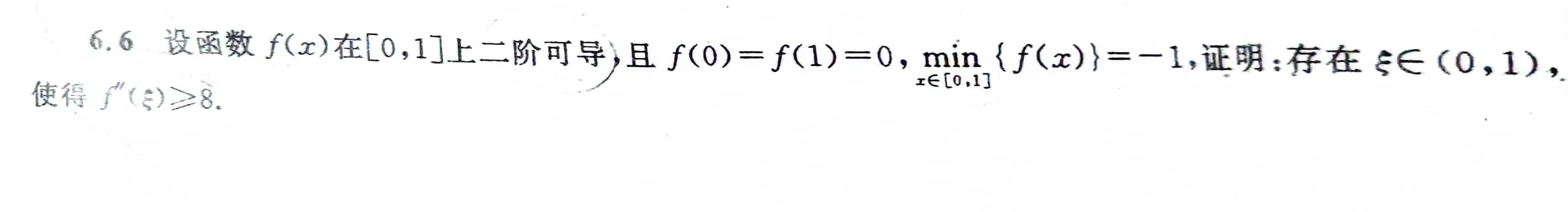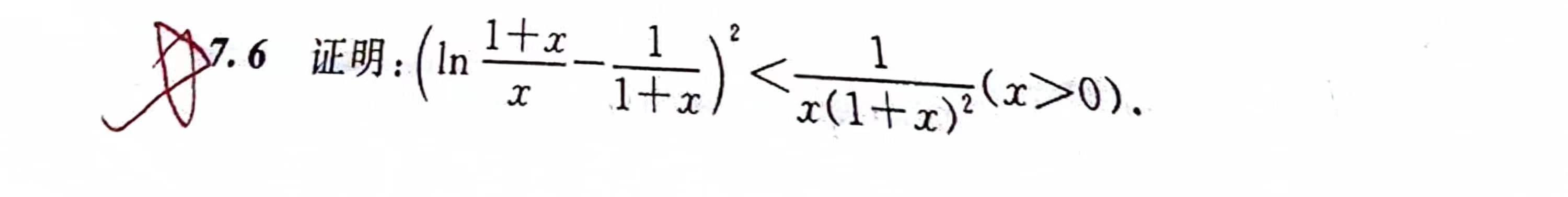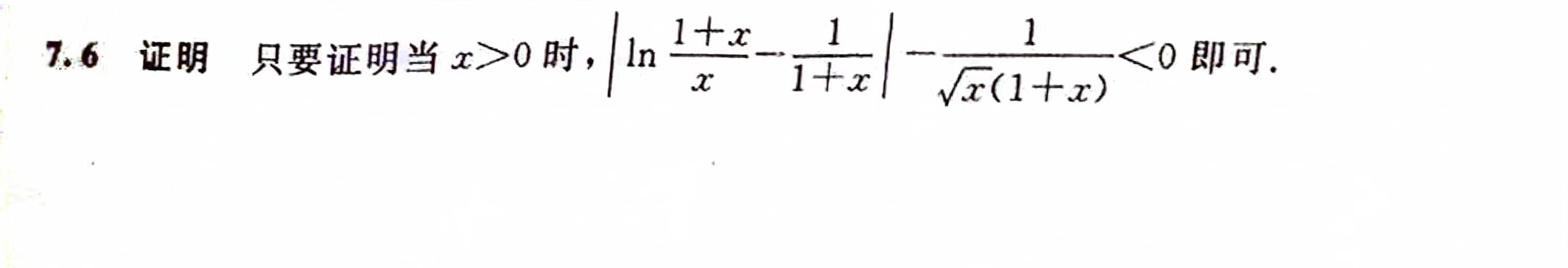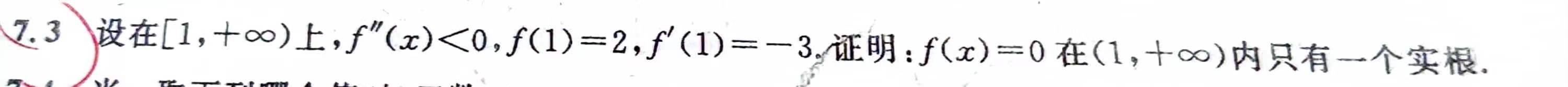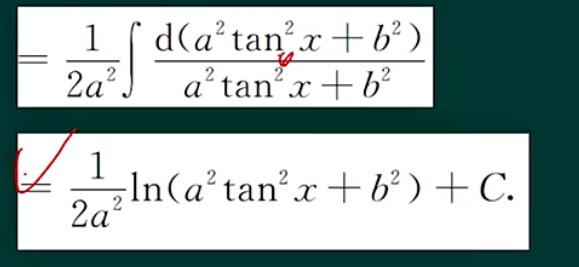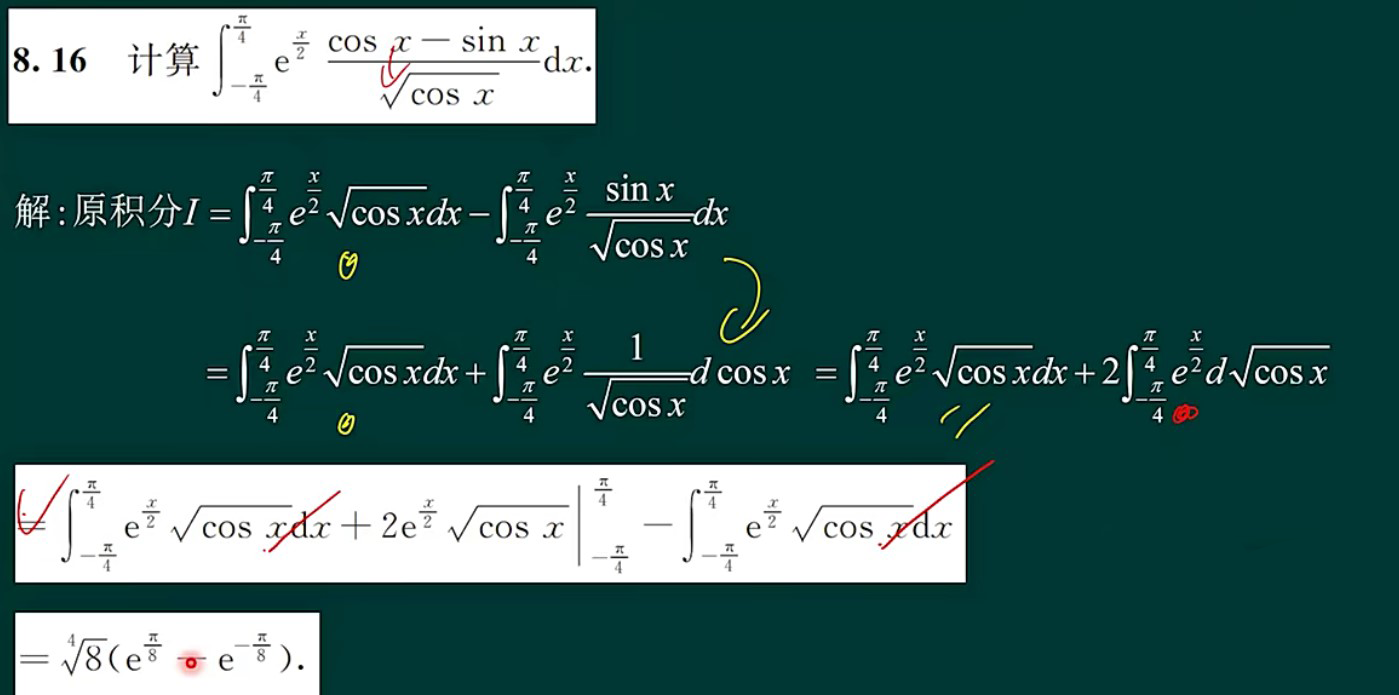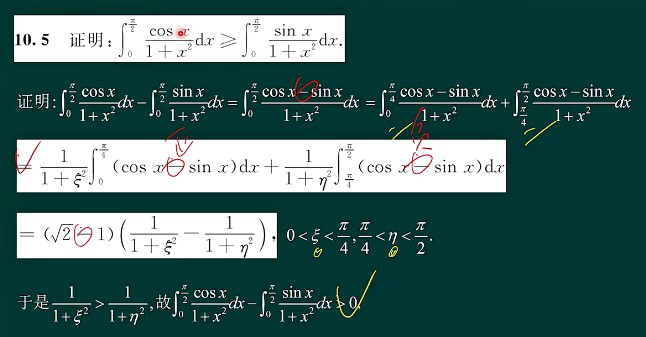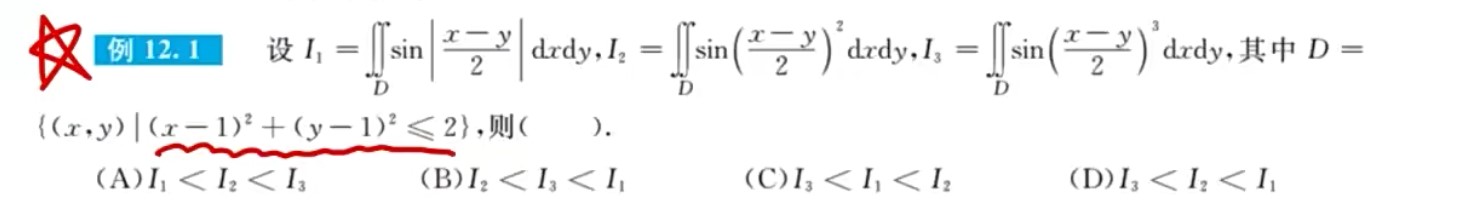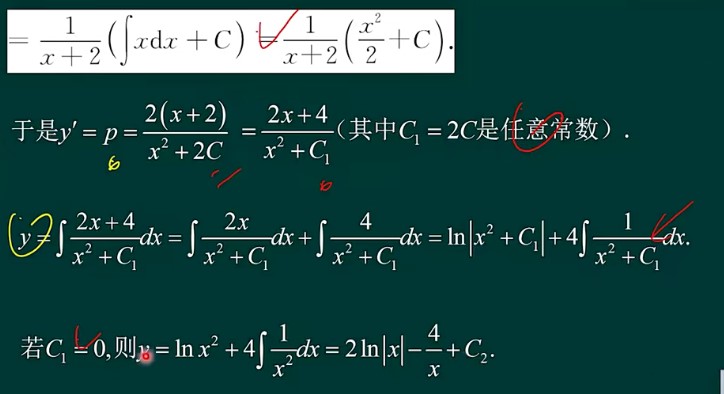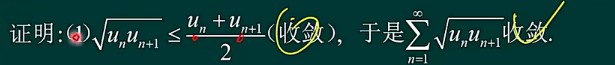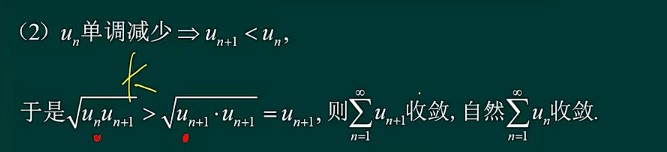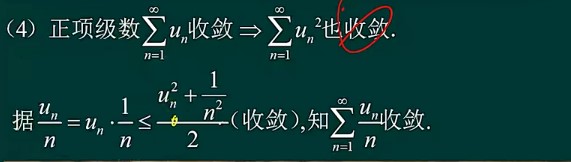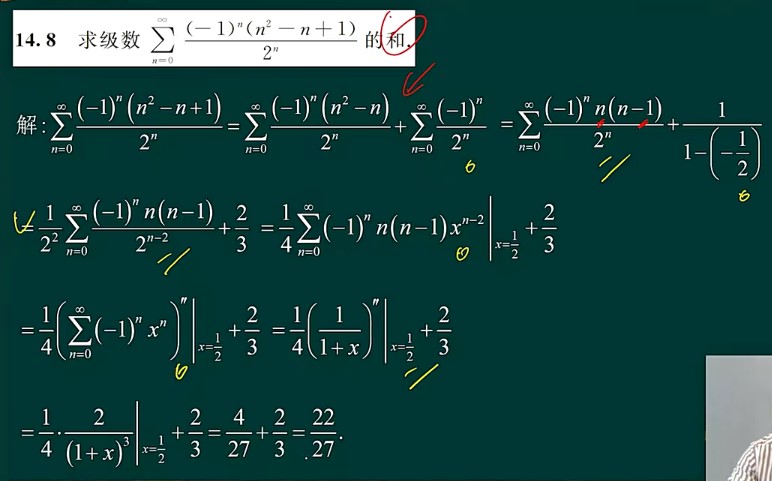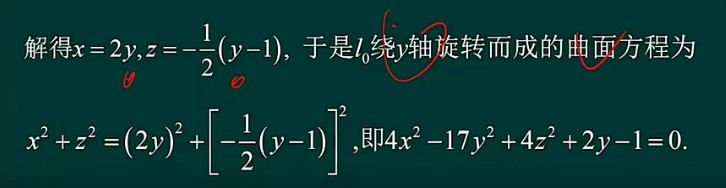高数错题本
函数
1
2
3
数列极限
1
2
函数极限
1
2
3
一元函数微分学的概念与计算
1
2
一元函数微分学的几何应用
1
2
中值定理
1
2
- 出现三个不同点的值时,两两之间使用拉格朗日中值定理
3
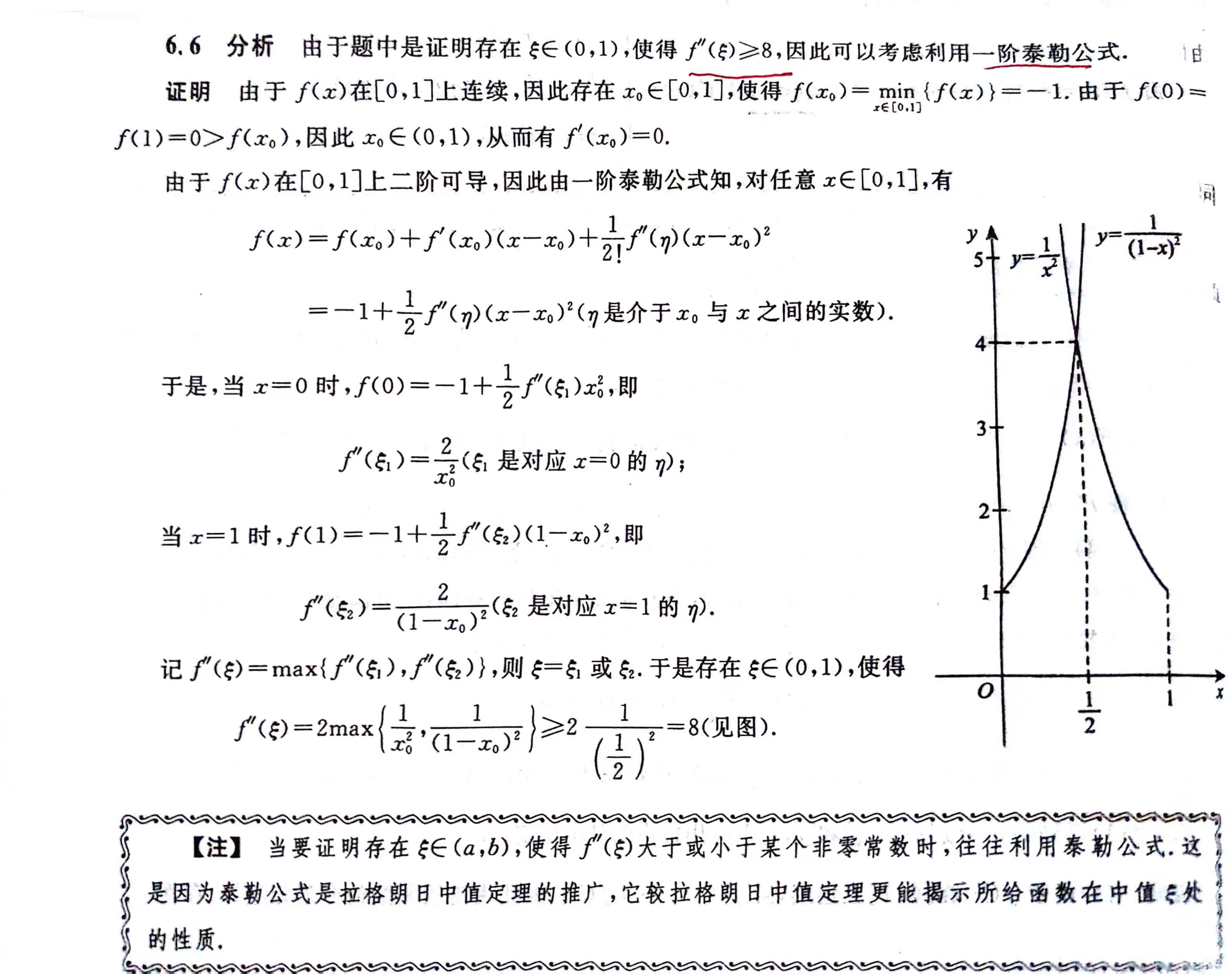
- 高阶导数用泰勒公式,,或者多次拉格朗日,三阶导数通过二阶导数用平均值,如果三阶导数不连续,则用导数介值定理
4
- 底为导数时可以尝试用柯西
5
- 当证明二阶导数大于或者小于某个非零常数时,往往利用泰勒公式
零点问题与微分不定式
1
2
3
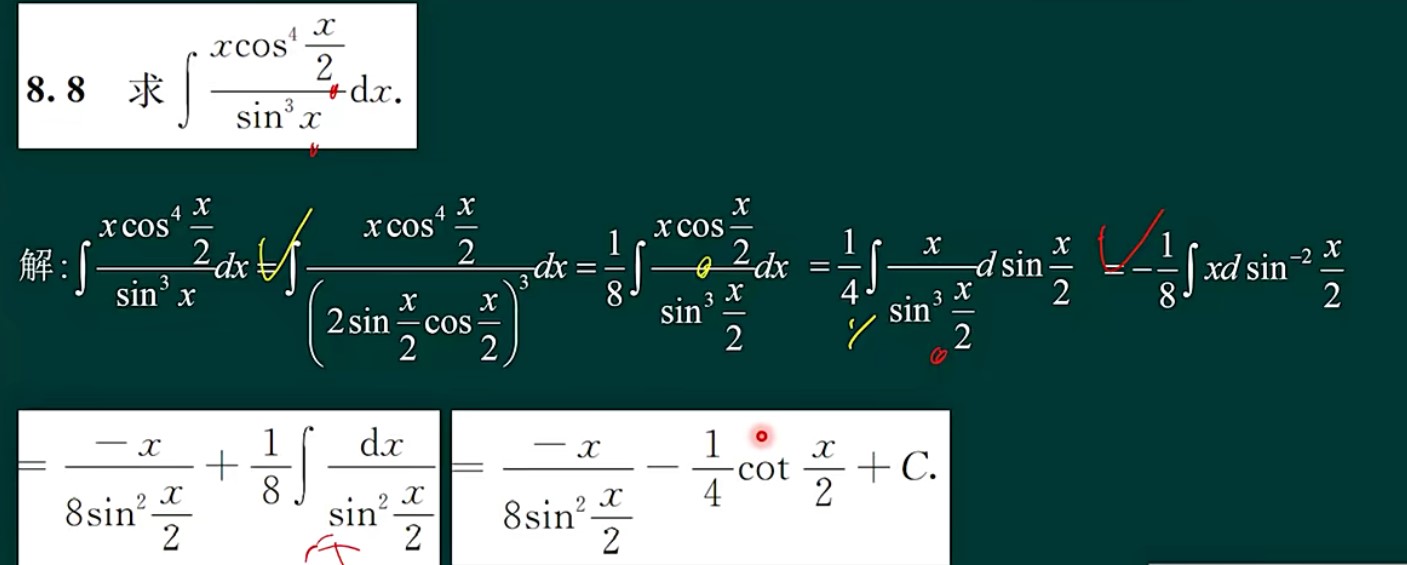
一元函数积分学的概念与计算
1
2
3
4
5
6
7
- 括号里面是复杂的参数,直接替换成u
8
- a=b=(a+b)/2
积分等式与积分不等式
- 端点为0考虑用拉格朗日
- 出现三个点,考虑两两之间用拉格朗日
1
- 含参数的考虑把参数变成x然后移项构造新函数
2
- 被积函数带导数或带变限积分时,考虑分部积分
- 证明题出现定积分,考虑用:
- 区间再现
- 中值定理
- 分部积分
3
- 出现积分与函数加减运算,一般二者统一化,变成积分加积分或者函数加函数
- 证明积分不等式可以考虑变上限或者下限为参数,构造变限积分进行求导
4
5
6
7
- 证明题结论中被积函数有导数,走牛顿莱布尼兹公式,没有就用拉氏
多元函数微分学
1
- 找区域上的最大值和最小值分两步:
- 找区域内部可疑点,导数为0,导数不存在
- 找边界上的可疑点,导数为0,导数不存在
2
- 技巧:
3
- 二元函数的驻点:对x的偏导数和对y的偏导数均为0
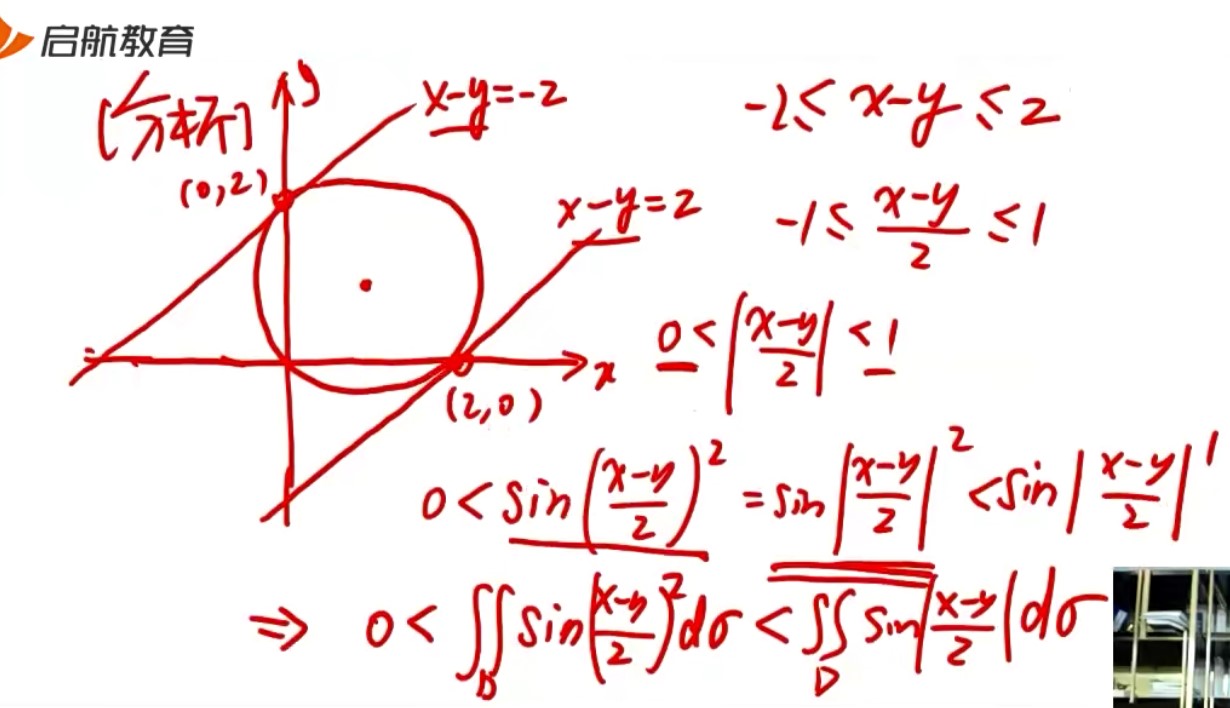
二重积分
1
2
3
常微分方程
1
2
3
4
- 非齐次的解由齐次的解和非齐次的解共同构成,通解代表每个解,通解都由两个解构成代表每个解都由两个解构成,所以特解有可能由非齐和齐次构成,得找出齐次的和非齐次的部分
TIPS:
5
- 非齐次的两个解做差是齐次方程的非零解,几阶就有几个常数,如果找非齐次的通解就是齐次的通解加上非齐次的特解
6
7
8
9
- 二阶、高阶的题每一次出现常数,尽快把常数定下来,不要带着C往下走
10
- 考三次,考四次一定是特殊的能因式分解
无穷级数
1
2
- 比较复杂的级数要研究通项
- 只有正向级数才能等价替换
3
- 有根号就有理化
4
- 级数求和,能拆即拆,一个个做
- 没有x就创造x
5
6
7
8
- 通项是积分表达式,积不出来的,一般放缩积分然后进行处理(分母变小、分母拿掉)
10
- 根号:通分、约分、有理化、换元、提公因子
11
12
- 研究绝对收敛和条件收敛还可以拆分
13
- 求和先求收敛域和收敛范围
- 求和技巧:拆开求、分开求;求导消分母,积分还原
- 幂级数的和函数都是连续函数
14
- 没有x的级数求和就创造x,把常数改成x
微积分应用
1
- 液体质量公式
- 功的物理公式
- 压力的物理公式
- 引力的物理公式
- 行星的物理公式
- 上减下,右减左代表距离
- 常考:浸水压力、抽水做功、形心问题
2
3
4
5
- 改变有限个点的值,不影响积分的进行
6
- 级数看不懂就展开

多元函数积分学的基础知识
1
- 要找平面靠点和法向量(点法式)
- 与两条直线垂直的法向量即两条直线的向量叉乘
2
-
直线在面上的投影,就是过该直线找一个与平面垂直的平面,然后联立,二者的交线即是直线在面上的投影(利用平面束的思想)
- 把直线改成一般式,构造平面束(一个不变另一个前面加λ)
- 法向量内积=0(垂直)得出λ
- 联立垂直面和题目面得出交线
-
绕哪个轴转,就解出其他两个变量和该轴变量的关系
-
其余两个变量平方相加,左右相等
3
4
5
6
三重积分
1
2
- 见到有取不到的点,即涉及偏导数不连续的点,先看能不能代入消掉分母(曲线积分和曲面积分),代不进去再挖。
- 曲线积分和曲面积分化为二重积分或者三重积分以后包括内部空腔,不能把边界的曲面或者曲线积分代进去,只能在曲线积分或者曲面积分的时候代入
3
- 碰到空间曲线喜欢抓参数方程ttt,没有参数方程就构造参数方程
- 空间曲线优先参数方程,其次斯托克斯
4
- z在两个水平面之间,被积函数只跟z有关,这种三重积分适合先二后一法
5
- 曲线积分和曲面积分都可以把方程本身代进去
6
7
- 曲面四面八方都对称,只要出现奇函数都是0
8
- 只要是x的一次方或者y的一次方或者z的一次方或者同时出现都是一次方,作二重积分或者三重积分或者第一型曲线积分或者第一型曲面积分,有技巧,即形心技巧
- x/y/z的积分可以转化为形心*对应几何量
- 二重面积,三重体积,曲线长度,曲面面积
- 形心就是图形的中心
9
10
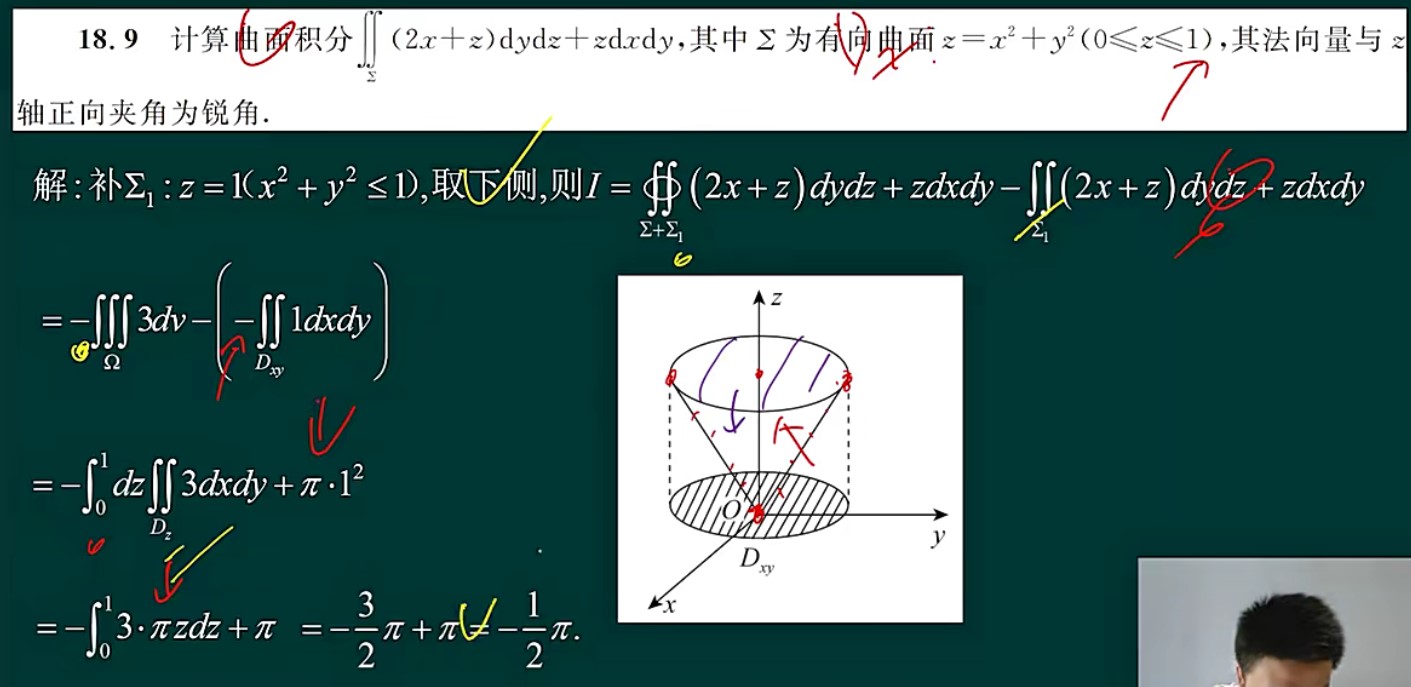
- 第二型曲面积分补面的时候,要保持方向一致,都朝内或者都朝外,指向内部空腔,高斯公式为负,背离内部空腔,高斯公式为正
- 下侧往下投是负的,上侧往下投是正的
11
12
- 涉及dz,说明是空间曲线
- 空间曲线首选直接法或者说参数法,即把曲线方程爆改参数方程,即改成与t相关
- 联立消掉另一个变量
- 顺时针派到负派,逆时针负派到派
- 空间曲线首选直接法或者说参数法,即把曲线方程爆改参数方程,即改成与t相关
13
- 斯托克斯公式就是化线为面,曲线选一次方的,选最简单的,选平面
- 选方向用右手定则选法向量
- 投影:联立方程组消掉z
高数错题本
http://example.com/2024/04/15/高数错题本/